【数式なしで徹底解説!】機械学習の基本!回帰分析(単回帰分析・重回帰分析)について解説します! では、機械学習を用いてデータ解析やデータの予測を行う際に、もっとも一般的な解析手法の一つである回帰分析についてご説明します。
最近、「AI」や「機械学習」という言葉をよく聞きますよね。
でも多くの方はこれがどのような仕組みで動いているのかはご存知でないかと思います。
詳細な説明は他の専門サイトに譲るとして、ここでは数式などは省いて視覚的に理解していただけるようにざっくりとご説明していきたいと思います。
私自身、物事を理解する際には、数式などよりもイメージで原理を理解することを大事にしていますので、ここでもそのイメージについてなんとなくでもご理解いただけるようにご説明していこうと思います。
イメージだけでも知っていると、ちまたで耳にするニュースの捉え方が格段に変わります。
数式などの詳細な説明については、いくつかリンクを貼っておきます。
「原理からしっかりと理解したい」という方はこちらをご参考ください。
回帰分析は、大きく分けると2種類あります。
単回帰分析と重回帰分析です。
さらには内挿と外挿に関する理解も重要です。
それでは順番にご説明していきます。
目次
【数式なしで徹底解説!】機械学習の基本!回帰分析(単回帰分析・重回帰分析)について解説します!

1. 回帰分析とは
まずは機械学習の基本となる回帰分析についてご説明します。
回帰分析とは、一言でいいますと「過去のデータを基づいて、次にくる値を予測する分析手法」です。
数式はなるべく使いたくないので、ここでは図を利用して視覚的にご説明していきますね。
例:年齢と収入の関係
イメージしやすいように身近な例で考えてみましょう。
例えば年齢と収入の関係について考えてみます。
今の時代は昔ほどとまでは言えませんが、大体年齢が上がるとともに収入も増加していく傾向にありますよね。
ざっくりと適当に書いただけですが、例えば街頭アンケートをとったところ、次のような年齢と年収の分布が得られたとします。
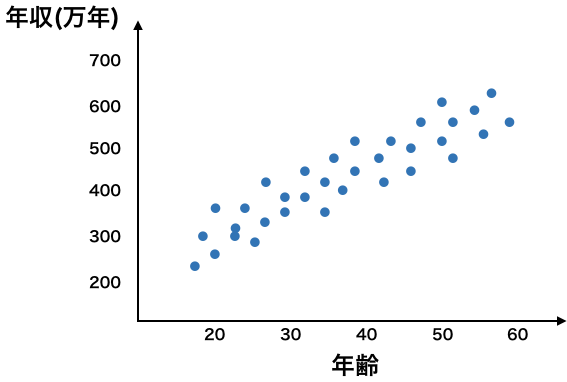
これから何がわかるかといいますと、年齢と年収の間にどのような関係があるかがわかりますよね。
結果の分布図からわかることは、「年齢が上がるにつれて年収も増加する」ということです。
この分布を利用すれば、次にくるアンケート結果をざっくりと予測することができます。
例えばアンケートで次に尋ねる方の年齢が35歳であるとすると、これまでの結果から、大体400万円ちょっとくらいかなと予測できるわけです。
これが回帰分析です。
つまり回帰分析とは「これまでに蓄積したデータを基に、次にくるデータを予測する」ということになります。
実際には機械がグラフから読み取ることは難しいので、この分布図を基に、年齢と収入の関係を示す数式を求めることになります。
これまたイメージですが、おおよそこのような関係になるのではないでしょうか。
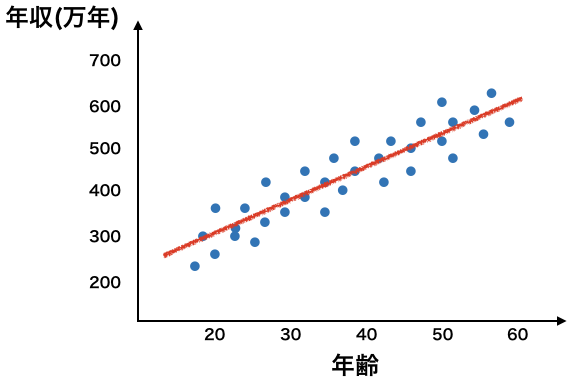
この赤線で描かれた線を数式にすることができれば、ある年齢を入力するとその方の年収を予測することができます。
これが回帰分析です。
さらにこの逆の予想も可能になります。
つまり、年収を聞くだけで大体の年齢を予測できるようになります。
ただもちろん図を見ていただくとわかりますように、必ずしも予測は一致しません。
必ず誤差は発生します。
つまり、この年齢と収入の関係を完全なぴったり予測をすることは不可能であるということです。
仮に誤差がないとどのような事態になるのでしょうか。
それは「ある年齢の方は必ずこの年収になると決定づけられる」ということになります。
例えば、25歳の人は全員年収270万円、40歳の方は全員440万円といった具合です。
そんなことありえませんよね(笑)
実際の世界には、25歳でも年収300万円の人もいれば、500万円の人もいます。
1000万円の超える方も少なからず存在します。
したがいまして、回帰分析を応用してある値を予測する際には、必ず誤差が発生します。
完璧な予測はできません。
それでは、どのようにすればこの誤差を減らせるのでしょうか。
これについては、考慮するデータの種類を増やすことによってある程度減らすことができます。
こちらについては単回帰分析と重回帰分析のセクションでご説明します。
2. 単回帰分析とは
まずは単回帰分析です。
単回帰分析とは「1つの変数を利用する回帰分析」です。
上記の例のような、年齢と収入の関係を予想するモデルは、年齢だけを考慮して収入を予測しているので単回帰分析になります。
名前にも「単」という言葉があるのでなんとなく想像つきますよね。
単回帰分析は計算がシンプルで利用しやすいですが、前述の通り誤差が大きくなりがちです。
これを改善するためには考慮する要素を増やす必要があります。
これが次にご紹介する重回帰分析です。
3. 重回帰分析とは
重回帰分析とは、「複数の変数を利用する回帰分析」です。
先ほどの年齢と収入の例で考えますと、ここでは年齢だけを考慮して年収を予測していました。
重回帰分析では考慮する要素を複数にします。
収入に影響がある要素は年齢以外にどのようなものが考えられるでしょうか。
職業や役職はもちろん年収に直結しますよね。
男女格差がいまだに大きい日本では性別も影響するでしょう。
このような要素をすべて考慮して年収を予測すると、年齢だけを考慮した場合よりも、より正確に年収を予測することができるようになります。
正確な予測ができるということは、誤差が小さくなることを意味します。
さらに親の収入や留学経験の有無など様々な要素をさらに追加するとより複雑な予測ができるようになります。
ただ、注意しなくてはいけないことが、考慮する要素が増えれば増えるほど正確な予測ができるとは限らないということです。
要素の中に全く年収と関連がないものがあれば、それを考慮しても予測精度は上がりません。
当然といえば当然ですよね。
したがいまして、重回帰分析を行う際にはどの要素を考慮するのか十分に検討する必要があります。
4. 内挿と外挿
考慮する要素を検討することはとても大切ですが、回帰分析を行う際に重要な概念がもう一つあります。
それが内挿と外挿に関する問題です。
言葉だけを聞くとわかりづらいですよね。
私なりに頑張って噛み砕いてご説明しますと、「内挿は予測に利用するデータの範囲内に収まる値をもとに予測する、外挿は予測に利用するデータの範囲外に該当する値をもとに予測する」ということになります。
すみません。わかりづらいですよねw。
冒頭の年齢と年収の関係を例にご説明しますね。
先ほどの図をもう一度こちらに貼り付けます。

ここで注目するべきことは、データの範囲です。
ここではプロットされているデータの要素、つまり年齢と年収の範囲になります。
ざっくりで申し訳ありませんが、この図を見てみると、年齢のデータ範囲はだいたい17歳くらい〜60歳くらいであることがわかります。
年収は最低でだいたい220万円くらい〜最高で620万円くらいになります。
これらの範囲をもとに内挿と外挿についてご説明します。
内挿はこのデータ範囲内で予測することを意味します。
外挿はこのデータ範囲外で予測することを意味します。
図を使ってみてみましょう。
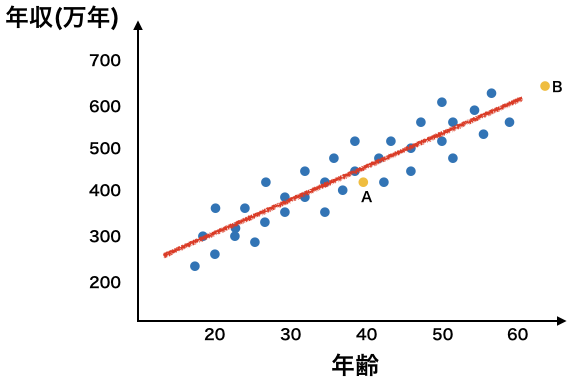
こちらのAが内挿、Bが外挿に該当します。
これでイメージがつきやすくなったのではないでしょうか。
例えば、Aの年収を予測するとします。
このとき年齢はおおよそ40歳、過去データ(水色のプロット)を合わせてみてみると、Aの年齢はこれまでに集められたデータの範囲内に収まっていることがわかりますよね。
40歳ぴったりの過去データがなくても30代のデータや40代のデータがあります。
このように、過去のデータの範囲内で予測することを内挿と言います。
内挿の場合は信頼できる予測ができるとされています。
一方で、Bについてみてみると、こちらのデータを予測する場合、まず年齢は65歳くらいでしょうか。
過去のデータ(水色のプロット)をみてみると、これまでのデータは最高でも60歳ほどで65歳のデータは含まれていないことがわかります。
このように、過去のデータの範囲外で予測することを外挿と言います。
外挿の場合は信頼できる予測ができません。
直感的には赤線で描いたモデルをそのまま延長していけば、だいたい65歳では年収600万円あたりと予測できるのですが、この信頼性は保証されません。
60歳を過ぎると退職する方が増えるので、収入は低下する傾向にあるかもしれません。
または最近の退職年齢引き上げの事情などから収入は横ばい、あるいは上昇する傾向になる可能性もあります。
過去データがない以上これらを予測することは信頼できないんですね。
これが外挿です。
したがいまして、回帰分析をする際には、予測に用いる要素が外挿に該当するのかを確認する必要があります。
もし外挿に該当する要素があるのであれば、その要素を除いて予測をするべきなのか、少しくらいの外挿値であれば問題ないのか、検討する必要があります。
何れにしても、外挿値を利用した場合には、その予測値の信頼性は下がります。
まとめ
いかがでしたでしょうか。
ここでは、機械学習の基本である回帰分析について、直感的に理解いただけるように数式なしでイメージのみでご説明してみました。
なんとなくてもご理解いただけましたでしょうか。
このイメージがつかめると、今後仮に数式を含めて本格的に勉強を始めたとしても理解しやすさが大きく変わると思います。
こちらの記事の説明が機械学習の理解をお助けができたら幸いです。
加えて、僕は機械学習に関する知識は全て独学で習得しています。
Udemyというオンライン動画学習ツールを利用して勉強しました。
色々なコースを受けてきましたが、機械学習の基礎を学ぶのであれば、「【キカガク流】人工知能・機械学習 脱ブラックボックス講座」が断然おすすめです。
説明能力が圧倒的に高くて、ど素人の僕でもすんなりと理解することができました。
初級編と中級編があります。上級編はまだないようですね。
ただ、こちらの記事でも紹介している通り、Udemyは定期的に大バーゲンセールを行なっているので、定価では購入しないでセールを待ったほうが良いです!
-

プログラミングの独学にUdemyをおすすめする理由!【僕はPythonを独学しました】




