【Pythonで株式投資】株価データからボリンジャーバンドを計算して可視化する【コード解説】

こんにちは。TATです。

今日のテーマは「【Pythonで株式投資】株価データからボリンジャーバンドを計算して可視化する【コード解説】」です。

Pythonを使って株価データを取得して、テクニカル分析ツールの1つであるボリンジャーバンドを計算する方法について解説します。

さらに計算結果をPlotlyを使っていい感じにチャートで可視化していきます。

Pythonコードもなるべくわかりやすく解説していきます。

ここで紹介しているコードは自由にコピっていただいてOKです。

【Pythonで株式投資】株価データからボリンジャーバンドを計算して可視化する【コード解説】

株価データの準備

まずは、ボリンジャーバンドを計算するために必要な株価データを準備します。

ここでは、yahoo_finance_api2を使って日経平均株価を取得します。

日足で過去3年分取得しました。

import sys
from yahoo_finance_api2 import share
from yahoo_finance_api2.exceptions import YahooFinanceError
import pandas as pd
 
my_share = share.Share('^N225')
symbol_data = None
 
try:
    symbol_data = my_share.get_historical(
        share.PERIOD_TYPE_YEAR, 3,
        share.FREQUENCY_TYPE_DAY, 1)
except YahooFinanceError as e:
    print(e.message)
    sys.exit(1)

df = pd.DataFrame(symbol_data)
df["datetime"] = pd.to_datetime(df.timestamp, unit="ms")

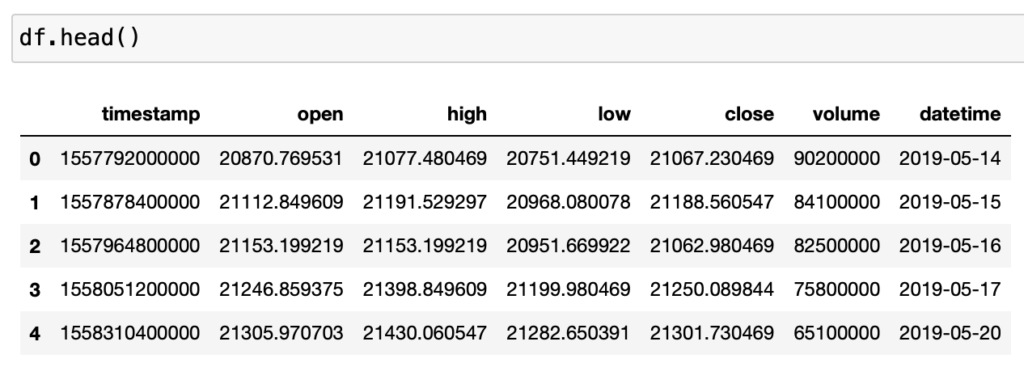
取得できたデータがこちらです。

yahoo_finance_api2を使った株価データの取得方法についてはこちらの記事で解説しています。

ボリンジャーバンドを計算する

株価データの準備ができたので、Pythonでボリンジャーバンドを計算していきます。

ボリンジャーバンドとは？

計算をする前に、まずはボリンジャーバンドについて簡単に解説しておきます。

ボリンジャーバンドは、テクニカル分析手法の1つで、移動平均線と標準偏差から構成されます。

ボリンジャーという名前は、考案者である米国の投資家ジョン・ボリンジャーから来ています。

移動平均線と、その上下に移動平均線と標準偏差から計算した値動きの幅を示す線を加えて、統計学に基づいて「ほとんどの確率で株価がこの上下の線の内部に収まる」ということを示します。

この上下の線が帯（英語でバンド, Band）のように見えることから、ボリンジャーバンドと呼ばれます。

この帯は、拡大したり収縮したりするので、この動きをうまく活用すると売買ポイントを見極めることができます。

順張りと逆張り、どちらに利用できるのも大きな特徴です。

ボリンジャーバンドの計算方法

正規分布の特徴を活かして、株価の移動平均線をm、標準偏差をσとすると、m±2σあるいはm+3σを計算して可視化したものがボリンジャーバンドです。

正規分布では、平均値と標準偏差から全体のデータの割合を計算することができます。

m±2σであれば、データ全体の95.45%が収まるという意味になります。

この特徴を活用すれば、株価がどの範囲で動くのかを予測することができるようになります。

よって、計算するには移動平均線と標準偏差を計算して、それらからm±2σなどを計算すればOKです。

多くのケースではm±2σが使われますが、m±3σが使われるケースもあります。

Pythonで実装する

Pythonでボリンジャーバンドは結構あっさり計算できます。

rolling関数を使えば、任意の期間の移動平均線と標準偏差が計算できます。

これを使ってをm±2σあるいはm±3σ計算すればOKです。

ここではどちらも計算してみます。

移動平均線の期間は25日としました。

# 移動平均線
df["SMA25"] = df["close"].rolling(window=25).mean()

# 標準偏差
df["std"] = df["close"].rolling(window=25).std()

# ボリンジャーバンド
df["2upper"] = df["SMA25"] + (2 * df["std"])
df["2lower"] = df["SMA25"] - (2 * df["std"])
df["3upper"] = df["SMA25"] + (3 * df["std"])
df["3lower"] = df["SMA25"] - (3 * df["std"])

とてもシンプルなコードですね。

これでボリンジャーバンドの計算はOKです。

ボリンジャーバンドをチャートで表示する

ボリンジャーバンドの計算が完了したので早速チャートで表示してみます。

今回はPlotlyを使ってチャートを作っていきます。

いろいろな表示法をお見せしていきます。

シンプルに線だけ表示する

まずは一番シンプルな方法です。

単純に線だけ表示します。

import pandas as pd
import plotly.graph_objects as go
from plotly.subplots import make_subplots
 
# 非表示にする日付をリストアップ
d_all = pd.date_range(start=df['datetime'].iloc[0],end=df['datetime'].iloc[-1])
d_obs = [d.strftime("%Y-%m-%d") for d in df['datetime']]
d_breaks = [d for d in d_all.strftime("%Y-%m-%d").tolist() if not d in d_obs]
 
# figを定義
fig = make_subplots(rows=2, cols=1, shared_xaxes=True, vertical_spacing=0.05, row_width=[0.2, 0.7], x_title="Date")
 
# Candlestick 
fig.add_trace(
    go.Candlestick(x=df["datetime"], open=df["open"], high=df["high"], low=df["low"], close=df["close"], name="OHLC", showlegend=False),
    row=1, col=1
)
 
# Volume
fig.add_trace(
    go.Bar(x=df["datetime"], y=df["volume"], name="Volume", showlegend=False),
    row=2, col=1
)

# SMA
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA25"], name="SMA25", mode="lines"), row=1, col=1)

# ボリンジャーバンド
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["2upper"], name="2σ", line=dict(width=1, color="red")),
    row=1, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["2lower"], line=dict(width=1, color="red"), showlegend=False),
    row=1, col=1
)

fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["3upper"], name="3σ", line=dict(width=1, color="blue")),
    row=1, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["3lower"], line=dict(width=1, color="blue"), showlegend=False),
    row=1, col=1
)


# Layout
fig.update_layout(
    title={
        "text": "日経平均の日足チャート",
        "y":0.9,
        "x":0.5,
    }
)
 
# y軸名を定義
fig.update_yaxes(title_text="株価", row=1, col=1)
fig.update_yaxes(title_text="出来高", row=2, col=1)
fig.update_yaxes(title_text="乖離率", row=3, col=1)

 
# 不要な日付を非表示にする
fig.update_xaxes(
    rangebreaks=[dict(values=d_breaks)]
)
 
fig.update(layout_xaxis_rangeslider_visible=False)
fig.show()

このコードで表示さえるチャートがこちらです。

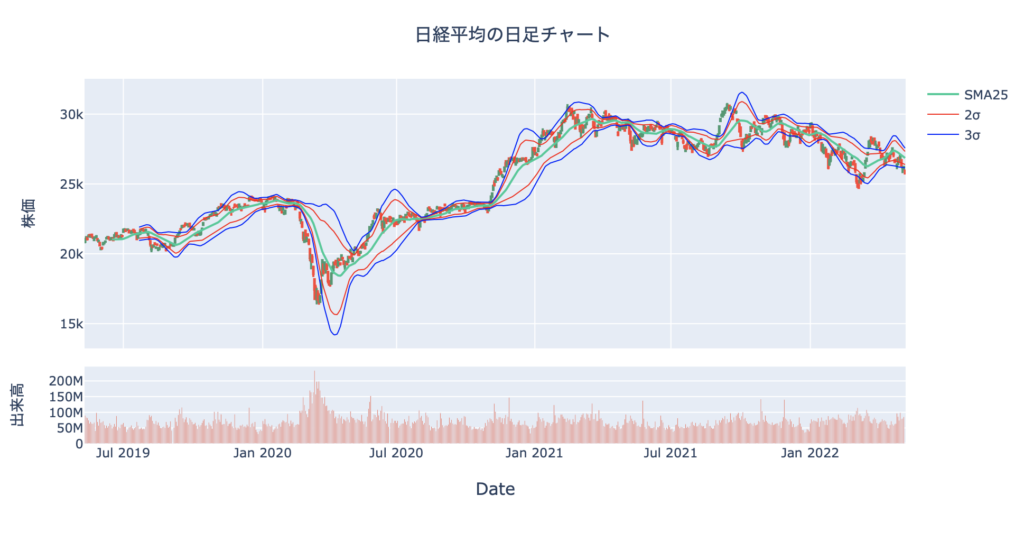
線だけでとてもシンプルですね。

2σと3σどちらも表示しました。

また、これらの線は±で2本ありますが、色を統一することでいい感じになります。

線の太さも少し細めに設定しました。

バンド（帯）をつける

次に少しかっこ良く見せるために帯をつけてみます。

import pandas as pd
import plotly.graph_objects as go
from plotly.subplots import make_subplots
 
# 非表示にする日付をリストアップ
d_all = pd.date_range(start=df['datetime'].iloc[0],end=df['datetime'].iloc[-1])
d_obs = [d.strftime("%Y-%m-%d") for d in df['datetime']]
d_breaks = [d for d in d_all.strftime("%Y-%m-%d").tolist() if not d in d_obs]
 
# figを定義
fig = make_subplots(rows=2, cols=1, shared_xaxes=True, vertical_spacing=0.05, row_width=[0.2, 0.7], x_title="Date")
 
# Candlestick 
fig.add_trace(
    go.Candlestick(x=df["datetime"], open=df["open"], high=df["high"], low=df["low"], close=df["close"], name="OHLC", showlegend=False),
    row=1, col=1
)
 
# Volume
fig.add_trace(
    go.Bar(x=df["datetime"], y=df["volume"], name="Volume", showlegend=False),
    row=2, col=1
)

# SMA
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA25"], name="SMA25", mode="lines"), row=1, col=1)

# ボリンジャーバンド
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["2upper"], name="2σ", line=dict(width=1, color="red")),
    row=1, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["2lower"], line=dict(width=1, color="red"), showlegend=False),
    row=1, col=1
)

# 帯をつける
fig.add_trace(go.Scatter(x=df["datetime"], y=df["2upper"], mode="lines", fill=None, line=dict(width=0, color="pink"), showlegend=False), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["2lower"], mode="lines", fill='tonexty', line=dict(width=0, color="pink"), showlegend=False), row=1, col=1)

# Layout
fig.update_layout(
    title={
        "text": "日経平均の日足チャート",
        "y":0.9,
        "x":0.5,
    }
)
 
# y軸名を定義
fig.update_yaxes(title_text="株価", row=1, col=1)
fig.update_yaxes(title_text="出来高", row=2, col=1)
fig.update_yaxes(title_text="乖離率", row=3, col=1)

 
# 不要な日付を非表示にする
fig.update_xaxes(
    rangebreaks=[dict(values=d_breaks)]
)
 
fig.update(layout_xaxis_rangeslider_visible=False)
fig.show()

表示されるチャートがこちらです。

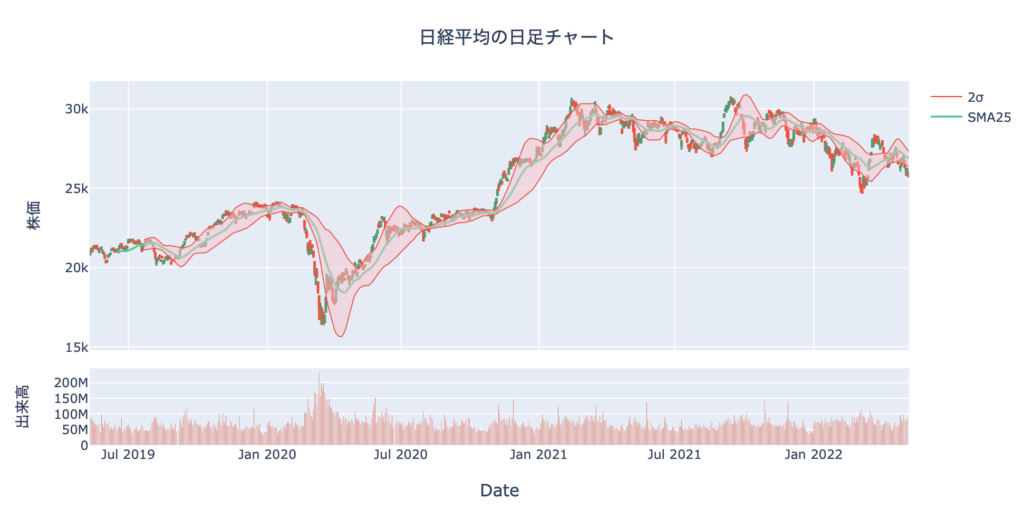
赤い帯をつけたので、帯の収縮や拡張が一目でわかりますし、どこで帯からはみ出したのかもすぐにわかりますね。

ここではm+2σのみを表示しました。

39〜40行目で帯をつけています。

fill='tonexty'を使うと、直前にプロットした線との間を塗りつぶすことができます。

ここでは2upperと2lowerの間を塗りつぶすという意味になります。

2σと3σどちらも帯をつけて表示する

最後に、m+2σとm+3σのどちらも帯をつけて表示してみます。

import pandas as pd
import plotly.graph_objects as go
from plotly.subplots import make_subplots
 
# 非表示にする日付をリストアップ
d_all = pd.date_range(start=df['datetime'].iloc[0],end=df['datetime'].iloc[-1])
d_obs = [d.strftime("%Y-%m-%d") for d in df['datetime']]
d_breaks = [d for d in d_all.strftime("%Y-%m-%d").tolist() if not d in d_obs]
 
# figを定義
fig = make_subplots(rows=2, cols=1, shared_xaxes=True, vertical_spacing=0.05, row_width=[0.2, 0.7], x_title="Date")
 
# Candlestick 
fig.add_trace(
    go.Candlestick(x=df["datetime"], open=df["open"], high=df["high"], low=df["low"], close=df["close"], name="OHLC", showlegend=False),
    row=1, col=1
)
 
# Volume
fig.add_trace(
    go.Bar(x=df["datetime"], y=df["volume"], name="Volume", showlegend=False),
    row=2, col=1
)

# SMA
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA25"], name="SMA25", mode="lines"), row=1, col=1)

# ボリンジャーバンド
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["2upper"], name="2σ", line=dict(width=1, color="red")),
    row=1, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["2lower"], line=dict(width=1, color="red"), showlegend=False),
    row=1, col=1
)

# 帯をつける
fig.add_trace(go.Scatter(x=df["datetime"], y=df["2upper"], mode="lines", fill=None, line=dict(width=0, color="pink"), showlegend=False), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["2lower"], mode="lines", fill='tonexty', line=dict(width=0, color="pink"), showlegend=False), row=1, col=1)

fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["3upper"], name="3σ", line=dict(width=1, color="blue")),
    row=1, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["3lower"], line=dict(width=1, color="blue"), showlegend=False),
    row=1, col=1
)

# 帯をつける
fig.add_trace(go.Scatter(x=df["datetime"], y=df["3upper"], mode="lines", fill=None, line=dict(width=0, color="lightblue"), showlegend=False), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["2upper"], mode="lines", fill='tonexty', line=dict(width=0, color="lightblue"), showlegend=False), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["2lower"], mode="lines", fill=None, line=dict(width=0, color="lightblue"), showlegend=False), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["3lower"], mode="lines", fill='tonexty', line=dict(width=0, color="lightblue"), showlegend=False), row=1, col=1)

# Layout
fig.update_layout(
    title={
        "text": "日経平均の日足チャート",
        "y":0.9,
        "x":0.5,
    }
)
 
# y軸名を定義
fig.update_yaxes(title_text="株価", row=1, col=1)
fig.update_yaxes(title_text="出来高", row=2, col=1)
fig.update_yaxes(title_text="乖離率", row=3, col=1)

 
# 不要な日付を非表示にする
fig.update_xaxes(
    rangebreaks=[dict(values=d_breaks)]
)
 
fig.update(layout_xaxis_rangeslider_visible=False)
fig.show()

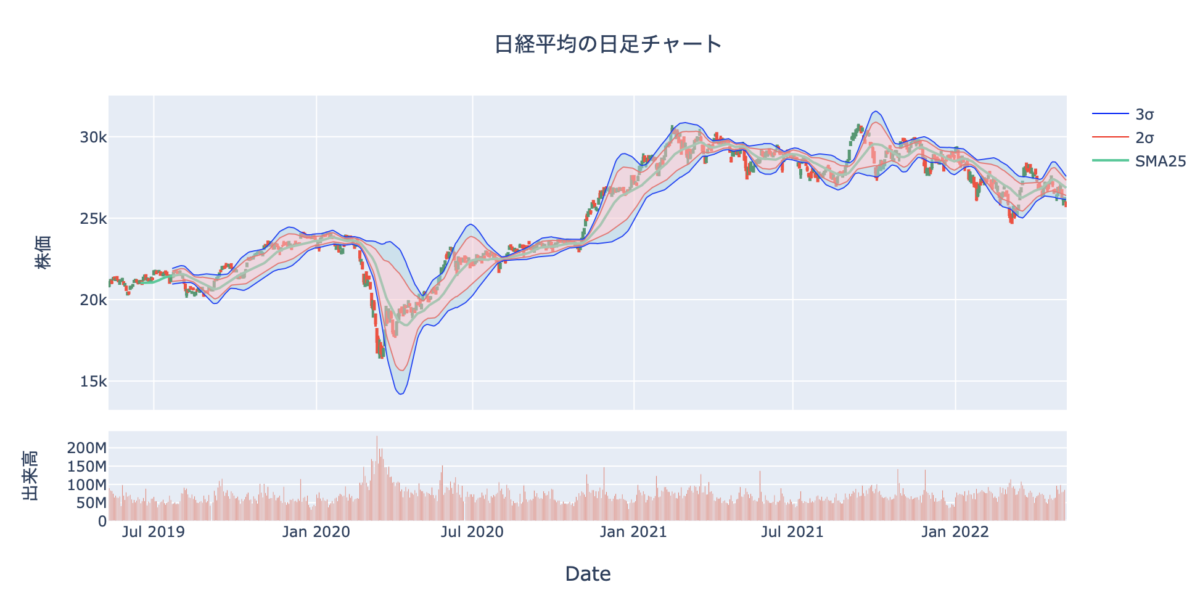
完成したチャートがこちらです。

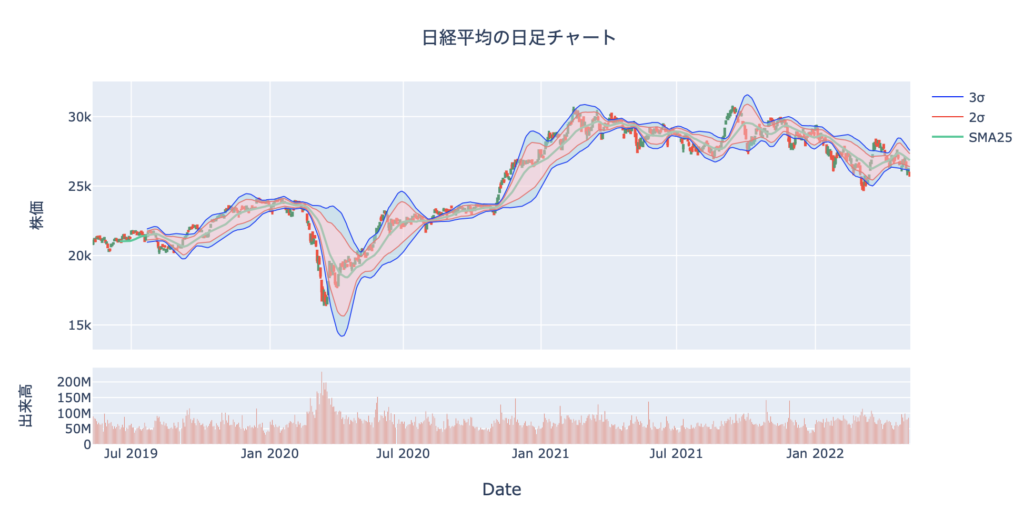
なんと言いますか、配色のセンスのなさが浮き彫りになってしまっていますが、とりあえず思っていたチャートが描けたのでこれでよしとしますw

先ほどの赤い帯に加えて青い帯を追加しました。

fill='tonexty'を使って塗りつぶしています。

先ほどとのように3upperと3lowerの間を塗りつぶしてしまうと、2upperと2lowerで塗りつぶしている部分と重なってしまうので、2upperと3upper、2lowerと3lowerの間を塗りつぶすようにしました。（52〜55行目）

Plotlyを使うと、このようにきれいなチャートを描くことができるのでおすすめです。

データの分析・可視化にはPythonが最適！

本記事で紹介したコードは、全てPythonを使って書いています。

Pythonはデータの分析や可視化を得意とするプログラミング言語で、さらにAI関連のライブラリーも豊富で昨今のAIブームで需要が急拡大しています。

→ 【いますぐ始められます】データ分析をするならPythonが最適です。

また、Pythonは比較的学びやすい言語でもあります。

実際、僕は社会人になってからPythonを独学で習得して転職にも成功し、Python独学をきっかけに人生が大きく変わりました。

→ 【実体験】ゼロからのPython独学を決意してから転職を掴み取るまでのお話。 

Pythonの学習方法についてはいろいろな方法があります。

僕はUdemyを選びましたが、書籍やプログラミングスクールも選択肢になります。

→ 【決定版】Python独学ロードマップ【完全初心者からでもOKです】

→ 【まとめ】Pythonが学べるおすすめプログラミングスクール

→ プログラミングの独学にUdemyをおすすめする理由！【僕はUdemyでPythonを独学しました！】

まとめ

いかがでしたでしょうか。

ここでは「【Pythonで株式投資】株価データからボリンジャーバンドを計算して可視化する【コード解説】」というテーマで、Pythonでボリンジャーバンドを計算してチャートに表示する方法について解説しました。

Plotlyを使えば、綺麗なチャートをPythonで描くことができます。

帯をつけたり、いろいろなアレンジを加えることも可能です。

本記事で紹介しているコードはご自由にご利用ください。

そしてもしエラーとかあれば教えてください。

ここまで読んでくださり、ありがとうございました。