こんにちは。TATです。
今回のテーマは「Pythonで売上高やEPSの年間推移から回帰直線を計算してトレンドを判定する方法」です。
企業の売上高やEPSのデータのトレンドを把握する方法として回帰直線を利用する方法について解説します。
回帰直線が右上がりなら上昇トレンド、右下がりなら下落トレンド、横向きなら横ばいと判断することができます。
回帰直線は、Pythonを使えば数行のコードで簡単に計算することが可能です。
目次
回帰直線とは?
まずは今回利用する回帰直線について簡単にご紹介しておきます。
回帰直線のイメージ
Wikipediaには回帰の意味について次にように書いてあります。
回帰(かいき)とは一般にはもとの位置または状態に戻ること、あるいはそれを繰り返すこと。
Wikipedia「回帰」より引用
簡単に言えば、回帰直線とはある散布図の関係性を直線で表したものです。
Wikipediaからイメージをとってきました。
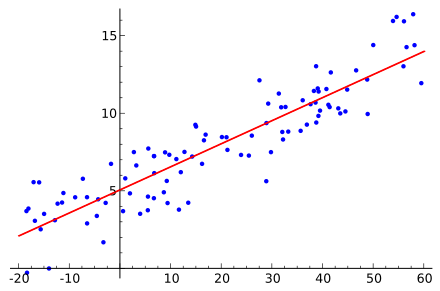
Wikipedia「線形回帰」より引用
こちらの散布図を見ると、右肩上がりの関係になっていることが想像できます。
そしてこの関係をビシッと直線で示したものが、赤線で示している回帰直線です。
式にすると y = a + bx と表すことができます。
中学校?で勉強した1次関数ですね。
aが切片、bが傾きになります。
回帰直線の求め方
次に回帰直線の求め方です。
これは最小二乗法を使って計算することができます。
ゴリゴリの数式はなるべく省いて、イメージで理解できるように解説します。
詳しい計算式については他サイトをご参照ください。
まずはイメージのために適当な散布図を用意します。
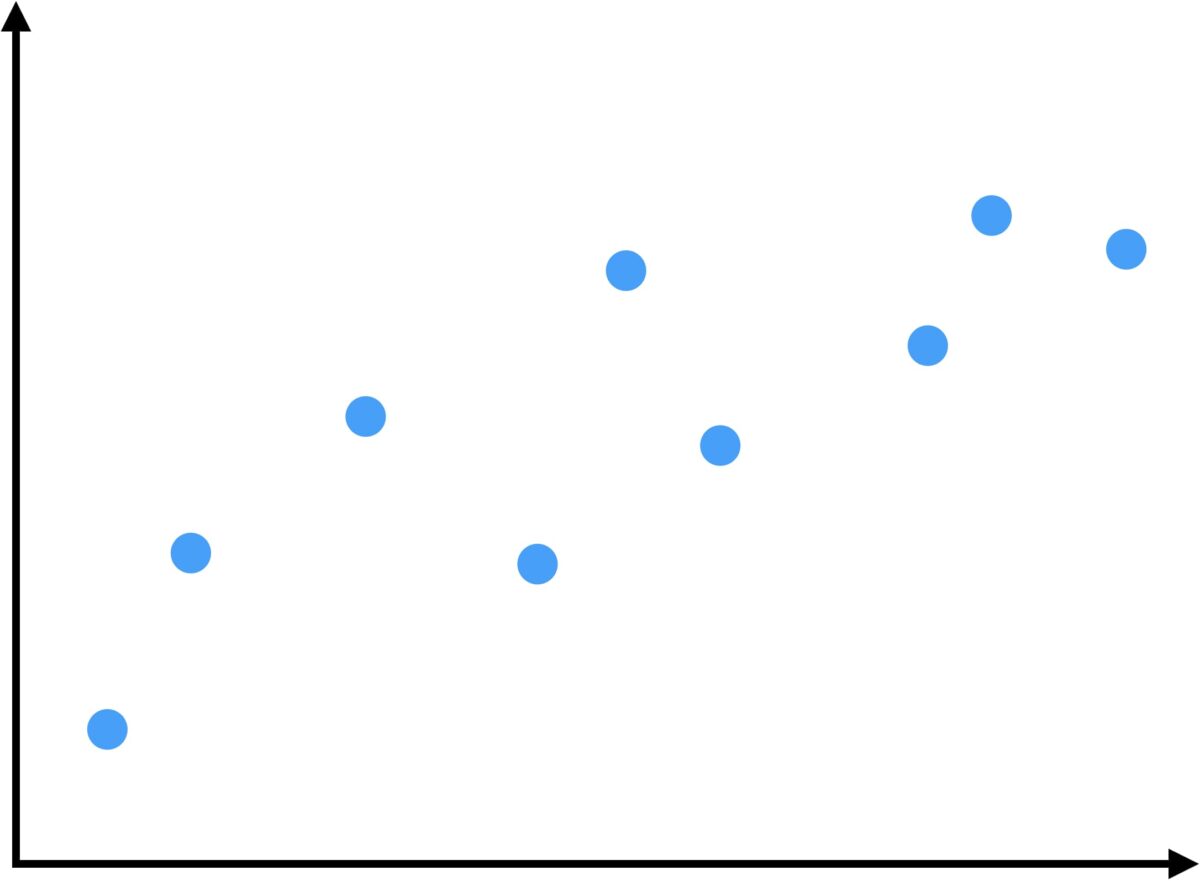
次に回帰直線をイメージするために、ここに適当にそれっぽい直線を引いてみます。
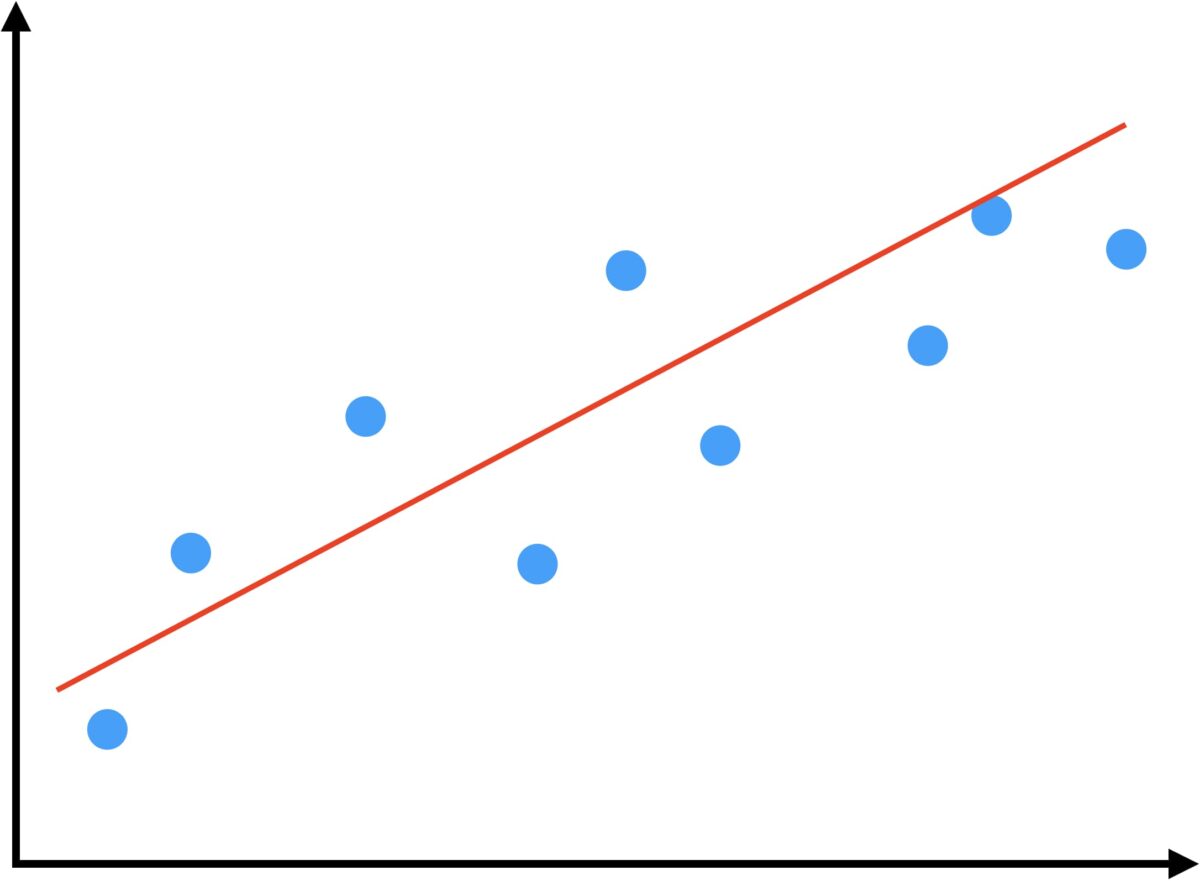
この直線が一番いい感じになるように計算していきます。
その手法が最小二乗法です。
そのためには、直線からそれぞれの点までの距離を計算します。(点線の部分)

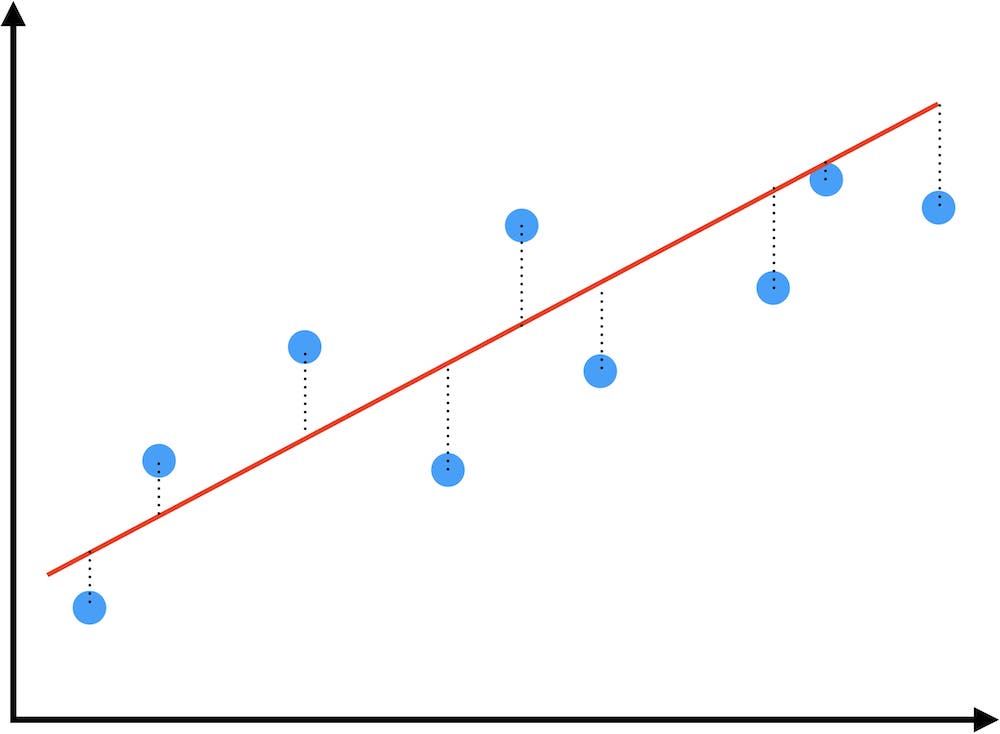
この距離はいわば誤差です。距離が大きくなれば誤差は大きいと考えることができます。
そしてこの距離(誤差)の合計が最も小さくなるような直線を求めることができれば、最も信頼性の高い直線であると判断することができます。
これが最小二乗法です。
誤差が最も小さくなるようにゴリゴリ計算して得られる結果が次の式です。
これらを使えば、 y = a + bx のaとbを計算することができます。
ポイント
b = (xとyの共分散) / (xの分散)
a = (yの平均) - b * (xの平均)
回帰直線から何がわかるのか
大切なのはここです。
回帰直線の計算式のついては、興味があれば理解しておいて損はありませんが、ぶっちゃけここで紹介する意味が理解できていれば十分実践で活用することができます。
回帰直線から何がわかるのか、簡単に言えば、次のことがわかります。
ポイント
- 傾きが正の数字なら上昇トレンド
- 傾きが負の数字なら下落トレンド
- 傾きがゼロに近いと横ばい
ただし、先ほどの誤差の大きさにも注意が必要です。
いくら最小二乗法で誤差が最も小さくなるようにしても、その数字自体が大きければ信頼性は低くなります。
ここを判断するためには相関係数が利用されたりします。
詳細は割愛しますが、ご興味あれば調べてみてください。(参照:Wikipedia「相関係数」)
本記事では相関係数は考慮せずに、純粋に回帰直線だけを計算していきます。
売上高やEPSの年間推移のデータから回帰直線を計算する
ここからが本題です。
売上高やEPSの年間推移のデータから回帰直線を計算してみます。
そしてその傾きがプラスなら上昇トレンド、マイナスなら下落トレンドと判断することができます。
これでトレンドを把握することができるようになります。
データの用意(例としてソニーのデータを使う)
まずはデータの用意です。
僕の場合、運営している「投資でニート生活」でXBRLデータを収集しています。(参考記事)
収集データをいい感じにまとめてnoteで提供したりもしているので、もしご興味あればご覧ください。
例として、ソニー(証券コード: 6758)の売上高とEPSのデータを用意します。
ここでは僕が独自に収集しているXBRLデータを使いますが、株探などのサイトからも簡単にデータを取得することができます。
業績データのテーブルをまるっとコピーしてエクセルに貼り付ければ簡単にデータを用意できます。
この記事を書いている2022年12月現在で、過去5年分+業績予想のデータを用意しました。
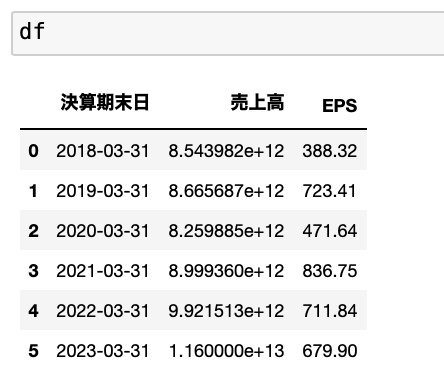
このデータを使って回帰直線を計算していきます。
-

PythonでTDNETとEDINETからXBRLデータを集めたら地獄だった話。
続きを見る
回帰直線の傾きと切片を計算する(numpyを使って計算)
Pythonで回帰直線の傾きと切片を計算する方法はいくつかありますが、ここではnumpyを使って計算します。
numpyのpolyfitを使うと回帰直線の係数(傾きと切片)を簡単に計算することができます。
例として売上高の回帰直線の係数を求めてみます。
coefficient = np.polyfit(df.index, df["売上高"], 1) print(coefficient)
![]()
polyfitでは、引数としてxとy、そして次元数を指定します。
ここでは次元を1としているので、1次元(線形回帰)になります。
配列の1つ目の数字が傾きで2つ目の数字が切片を意味しています。
ここでは傾きはプラスの数値になっているので、上昇トレンドと判断することができます。
傾きと切片にxを代入して回帰直線を計算する
次に求めた傾きと切片にxを代入して回帰直線を求めていきます。
これにはnumpyのpoly1dを使うと便利です。
次のコードでは、poly1dを利用してxに対するyを計算しています。
fit = np.poly1d(coefficient) fit(df.index)
![]()
これで回帰直線を計算することができました。
これをDataFrameに加えればOKです。
df["売上高_回帰直線"] = fit(df.index) df
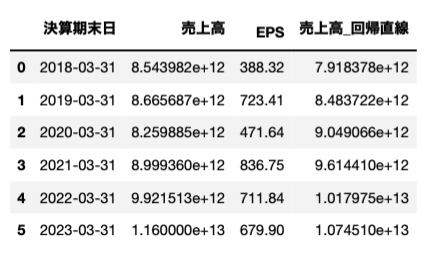
これで回帰直線を追加することができました。
同様にEPSの回帰直線も計算して加えます。
coefficient = np.polyfit(df.index, df["EPS"], 1) fit = np.poly1d(coefficient) df["EPS_回帰直線"] = fit(df.index) df
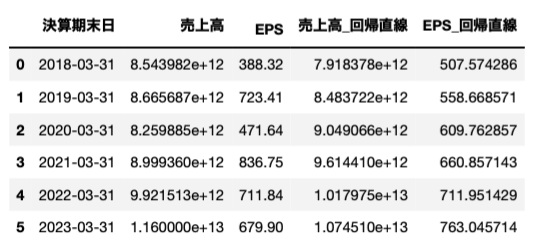
これで回帰直線の計算はおしまいです。
売上高とEPSの回帰直線を計算することができました。
売上高とEPSの回帰直線を可視化する
最後に回帰直線を可視化してみます。
今回は売上高とEPSの年間推移を棒グラフで可視化し、そこに回帰直線を加えます。
可視化用のライブラリとして、matplotlibを使います。
棒グラフに回帰直線を重ねて表示する
早速可視化していきます。
次のコードでは売上高を棒グラフで可視化し、そこに回帰直線を加えています。
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline
# チャートのサイズを定義
fig = plt.figure(figsize=(10, 5))
# 棒グラフの追加
plt.bar(df.index, df["売上高"])
# 回帰直線
plt.plot(df.index, df["売上高_回帰直線"], color="orange")
# x軸の値を決算期末日に変更
plt.xticks(df.index, df["決算期末日"])
# ラベル名を変更
plt.xlabel("決算期末日")
plt.ylabel("売上高")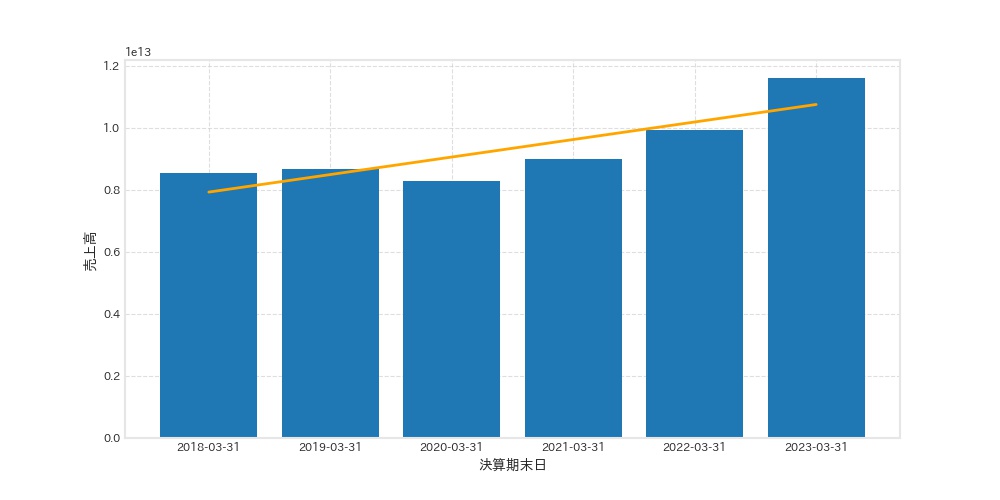
これで回帰直線をうまく可視化することができました。
右肩上がりになっているので、上昇トレンドであることがわかります。
チャートで可視化すると、 よりトレンドを把握しやすくなります。
-
【Python】matplotlibでグラフ目盛りの表示を変更する方法【xticks,set_xticklabels】
続きを見る
売上高とEPSの年間推移と回帰直線をまとめて可視化する
最後に、売上高とEPSの年間推移と回帰直線をまとめてチャートに可視化してみようと思います。
x軸を共有して両者を比較しやすいようにしました。
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline
# チャートの定義
fig, ax = plt.subplots(2, 1, figsize=(10, 10), sharex=True)
"""
売上高
"""
# 棒グラフの追加
ax[0].bar(df.index, df["売上高"])
# 回帰直線
ax[0].plot(df.index, df["売上高_回帰直線"], color="orange")
"""
EPS
"""
# 棒グラフの追加
ax[1].bar(df.index, df["EPS"])
# 回帰直線
ax[1].plot(df.index, df["EPS_回帰直線"], color="orange")
# x軸の値を決算期末日に変更
plt.xticks(df.index, df["決算期末日"])
# ラベル名を変更
plt.xlabel("決算期末日")
ax[0].set_ylabel("売上高")
ax[1].set_ylabel("EPS")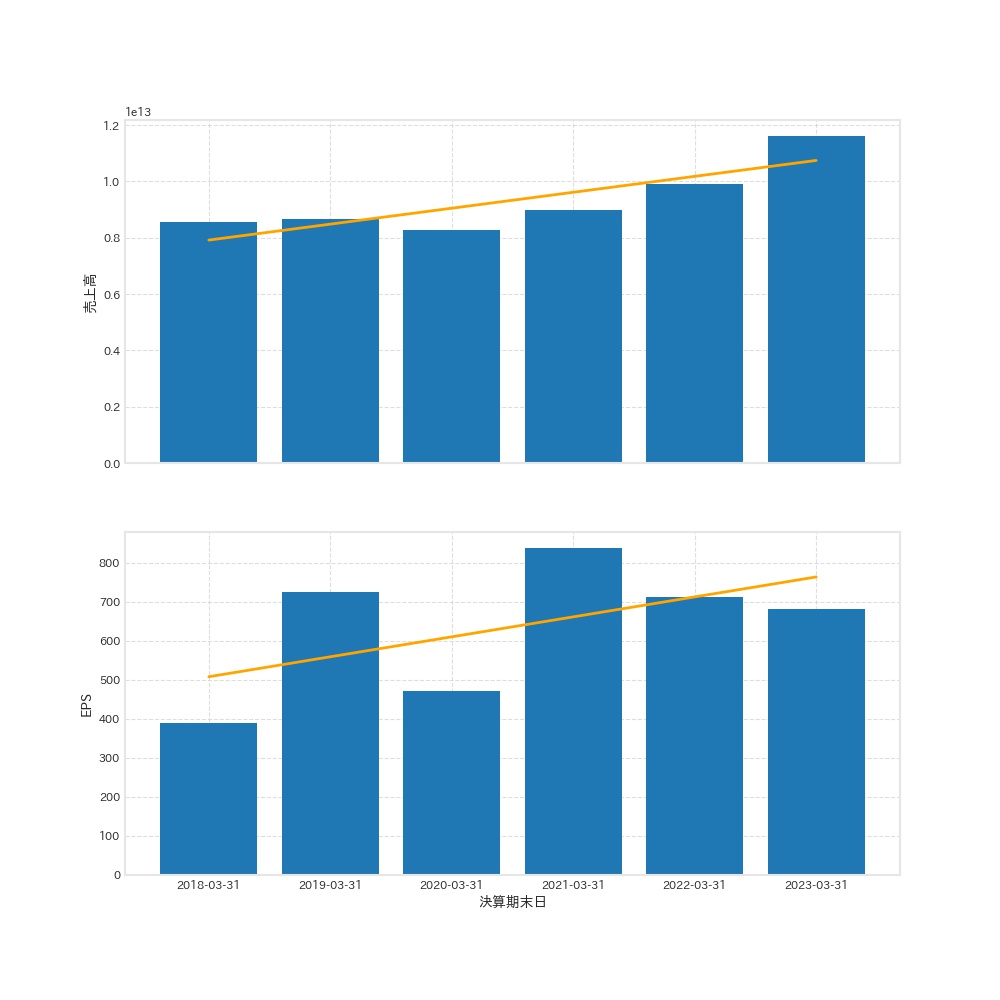
これで売上高とEPSをまとめて可視化することができました。
どちらも回帰直線も右肩上がりになっているので、上昇傾向にあると判定することができます。
このように、回帰直線を利用すればデータのトレンドを容易に把握することができるようになります。
さらに元データと併せてチャートで可視化することでより視覚的にトレンドを把握することができます。
(宣伝)noteでデータ提供中
最後にちょこっと宣伝です。
本記事で紹介した回帰直線を始め、特に日本株の成長株投資に必要な情報をまとめてnoteで発信しています。
基本的には、オニールやミネルヴィニの投資手法を参考にして、これを日本株に適用しています。
ここで必要な情報(株価チャート、決算情報など)を収集して、ないもの(レラティブストレングスやトレンドテンプレート)は独自にプログラムを開発して適用しています。
誰でもスクリーニングできるようにエクセル形式にデータをまとめたり、PDF形式にチャートや業績などの情報をレポートとしてまとめて提供したりしています。
もし興味あれば覗いてみてください。
本記事で紹介した売上高とEPSの年間推移の回帰直線もトレンドを把握するために使用しています。
スクリーニング条件としても活用しており、成長している銘柄のみをピックアップするようにしています。
まとめ
本記事では「Pythonで売上高やEPSの年間推移から回帰直線を計算してトレンドを判定する方法」について解説しました。
ここでは僕が独自に収集しているXBRLデータを利用してデータを用意しましたが、株探などのサイトを利用すれば簡単に業績データを入手することができます。
数値だけではわかりにくいですが、チャートに可視化することで傾向がわかりやすくなります。
そして回帰直線を利用すれば、トレンドをさらに容易に把握することができます。
PythonのNumpyを使えば、回帰直線を数行のコードで簡単に算出することができます。
銘柄をスクリーニングする際には、この回帰直線を利用して売上高が上昇傾向にある銘柄だけをピックアップする、みたいな条件を加えてみたりしても面白いかもしれません。
ここまで読んでくださり、ありがとうございました。