Pythonで株価の移動平均線乖離率を計算して「買われすぎ・売られ過ぎ」を判定する

こんにちは。TATです。

今日のテーマは「Pythonで株価の移動平均線乖離率を計算して「買われすぎ・売られ過ぎ」を判定する」です。

 

最近、Pythonに関する記事が増えつつあります。

単純にこっちの方が僕的に楽しいですし、アクセス状況を見ていると「Python×株式投資」に関する記事が圧倒的に人気なんですよね。

こういった分野で解説しているサイトは少ないと思うので、ニッチな需要を捉えられているのでしょうか。

こういう状況なので、今後「Python×株式投資」に関する記事は増やしていこうと思います。

 

話が逸れましたが、本記事ではPythonで移動平均線乖離率を計算する方法について解説し、そのデータを使ってどれくらい乖離すれば買われすぎ・売られすぎと判断できるのかを統計的に算出していきます。

最後は、計算結果をグラフで可視化して、買われすぎ・売られすぎのポイントがうまく機能するのかを見ていきたいと思います。

 

Pythonで株価の移動平均線乖離率を計算して「買われすぎ・売られ過ぎ」を判定する

データの準備

まずは必要なデータの準備です。

今回必要なデータは株価データです。

ここから移動平均線を計算して、さらに移動平均線乖離率を計算していきます。

 

株価データを取得する

株価データの取得方法については、本サイトで過去に解説しています。

• 【まとめ】Pythonで株価データを扱う
• 【Pythonコード解説】yahoo_finance_api2で日本株の株価データを取得する

 

今回はyahoo_finance_api2を使って株価データを取得します。

詳細は過去記事にありますので、ご興味あればご覧ください。

【Pythonコード解説】yahoo_finance_api2で日本株の株価データを取得する

続きを見る

 

サクッとコードだけご紹介しておきますね。

例としてトヨタ自動車の過去10年分の株価データを日足で取得します。

import sys
from yahoo_finance_api2 import share
from yahoo_finance_api2.exceptions import YahooFinanceError
import pandas as pd
 
my_share = share.Share('7203.T')
symbol_data = None
 
try:
    symbol_data = my_share.get_historical(
        share.PERIOD_TYPE_YEAR, 10,
        share.FREQUENCY_TYPE_DAY, 1)
except YahooFinanceError as e:
    print(e.message)
    sys.exit(1)

df = pd.DataFrame(symbol_data)
df["datetime"] = pd.to_datetime(df.timestamp, unit="ms")

 

このコードで取得したデータがこちらです。

最初と最後の5行を表示しています。

 

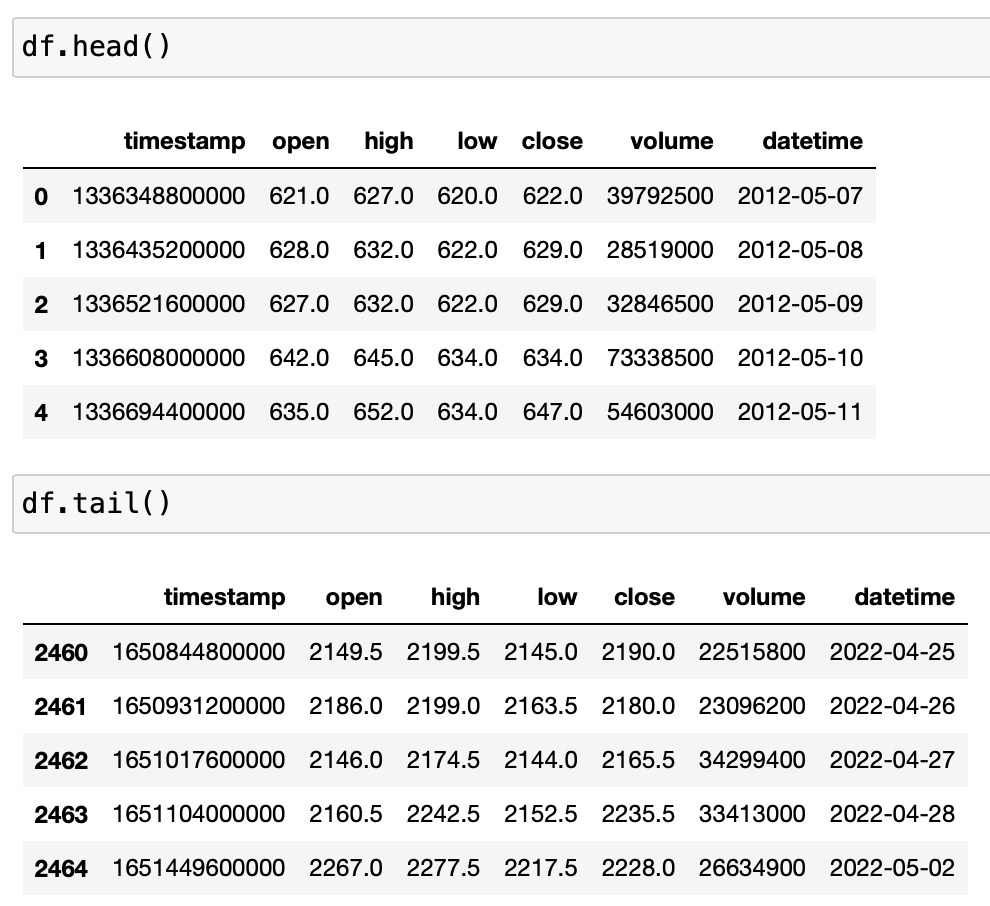
しっかり10年分取得できていることが確認できます。

そして10年で株価は3倍以上に上昇していますね。

 

このデータを使って移動平均線や移動平均線乖離率を計算していきます。

 

移動平均線を計算する

株価データが用意できたところで、移動平均線を計算していきます。

これがないと移動平均線乖離率を計算することはできませんから必須です。

 

移動平均線を計算する際に重要になってくるのが、どの期間を利用するかということです。

これは人によって変わってきます。

短期で見ているなら5日とか10日移動平均線を見るでしょうし、中長期になれば25日とか200日移動平均線とかを見る方が多くなると思います。

 

それぞれの投資戦略に合わせて適切に判断していただければ問題ないです。

ここでは、25日、50日、200日移動平均線を使っていきます。

 

移動平均線の計算方法については、過去記事で解説しています。

【コード解説】Pythonで株価データから主要なテクニカル分析を計算して可視化する【移動平均線、MACD、RSI】

続きを見る

 

rolling関数を使えば簡単に計算できます。

# 移動平均線
df["SMA25"] = df["close"].rolling(window=25).mean()
df["SMA50"] = df["close"].rolling(window=50).mean()
df["SMA200"] = df["close"].rolling(window=200).mean()

 

windowに任意の期間を指定すればOKです。

きちんと計算されていることが確認できます。

 

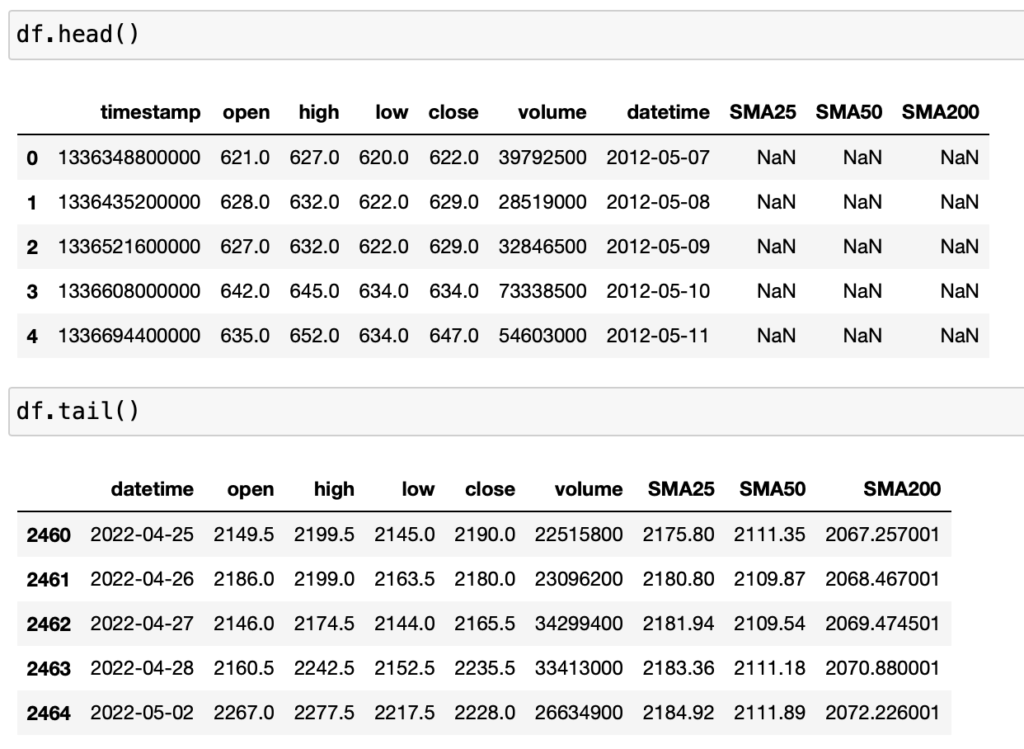
これで必要なデータは揃いました。

あとは、このデータを使って移動平均線乖離率を計算すればOKです。

 

チャートで可視化してみる

データの準備ができたところで、とりあえず一回チャートで可視化してみましょう。

この方法についても過去にご紹介しています。

• 【コード解説】Pythonで株価チャートを描く【mpl_finance編】
• 【コード解説】Pythonで株価チャートを描く【mplfinance編】
• 【コード解説】Pythonで株価チャートを描く【plotly編】

 

株価チャートを描くには色々なライブラリを利用することができますが、ここではplotlyを使って可視化します。

PythonのPlotlyでインタラクティブな株価のローソク足チャートを描く【コード解説】

続きを見る

 

詳細の解説は過去記事に委ねることにして、ここではコードだけご紹介します。

出来高と移動平均線も合わせて表示します。

 

import pandas as pd
import plotly.graph_objects as go
from plotly.subplots import make_subplots
 
# 非表示にする日付をリストアップ
d_all = pd.date_range(start=df['datetime'].iloc[0],end=df['datetime'].iloc[-1])
d_obs = [d.strftime("%Y-%m-%d") for d in df['datetime']]
d_breaks = [d for d in d_all.strftime("%Y-%m-%d").tolist() if not d in d_obs]
 
# figを定義
fig = make_subplots(rows=2, cols=1, shared_xaxes=True, vertical_spacing=0.05, row_width=[0.2, 0.7], x_title="Date")
 
# Candlestick 
fig.add_trace(
    go.Candlestick(x=df["datetime"], open=df["open"], high=df["high"], low=df["low"], close=df["close"], name="OHLC"),
    row=1, col=1
)
 
# Volume
fig.add_trace(
    go.Bar(x=df["datetime"], y=df["volume"], name="Volume"),
    row=2, col=1
)

# SMA
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA25"], name="SMA25", mode="lines"), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA50"], name="SMA50", mode="lines"), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA200"], name="SMA200", mode="lines"), row=1, col=1)


 
# Layout
fig.update_layout(
    title={
        "text": "トヨタ自動車(7203)の日足チャート",
        "y":0.9,
        "x":0.5,
    }
)
 
# y軸名を定義
fig.update_yaxes(title_text="株価", row=1, col=1)
fig.update_yaxes(title_text="出来高", row=2, col=1)
 
# 不要な日付を非表示にする
fig.update_xaxes(
    rangebreaks=[dict(values=d_breaks)]
)
 
fig.update(layout_xaxis_rangeslider_visible=False)
fig.show()

 

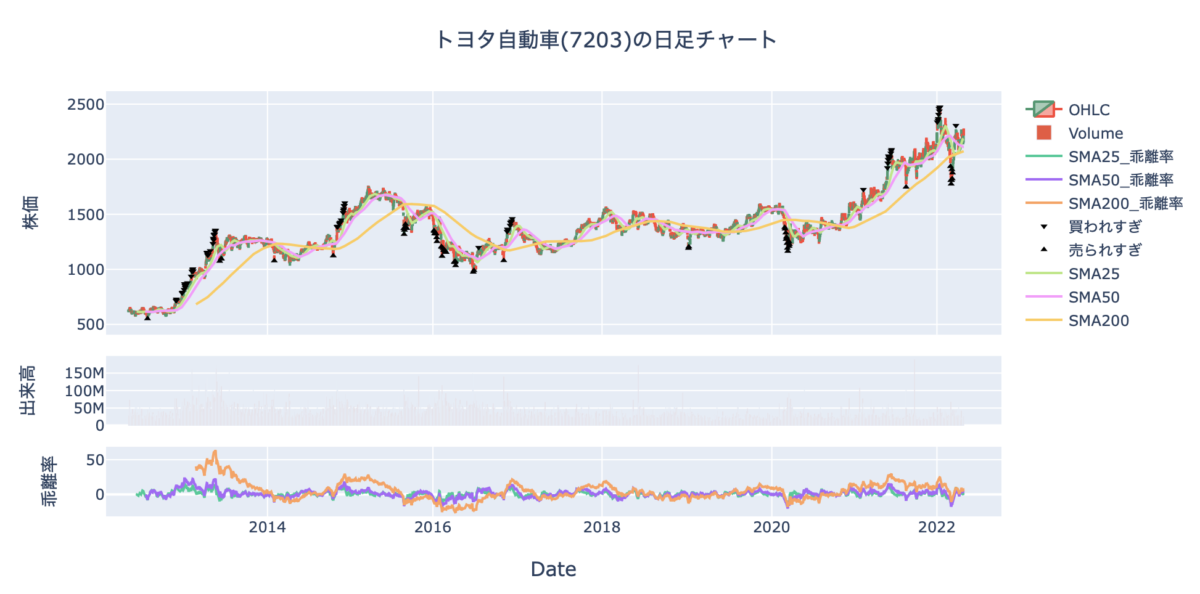
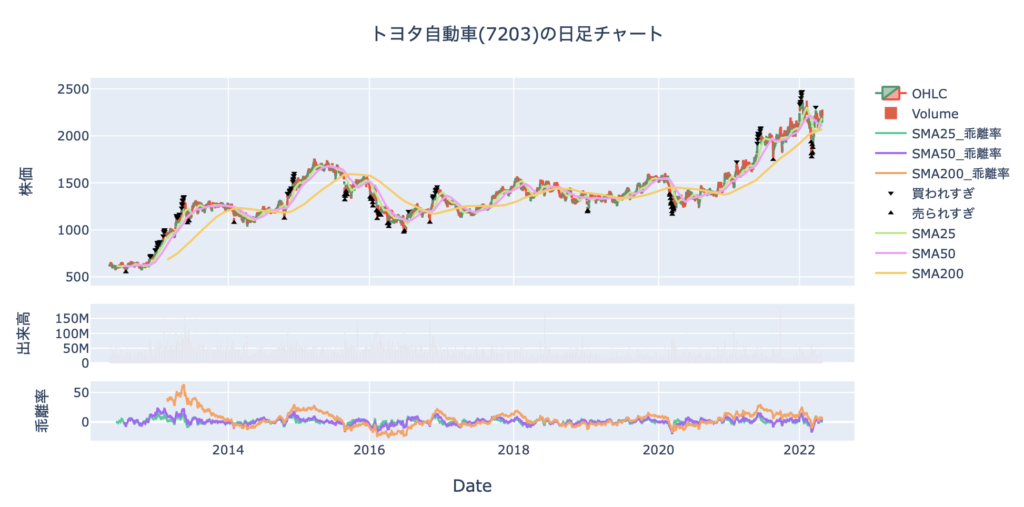
これで表示されるチャートがこちらです。

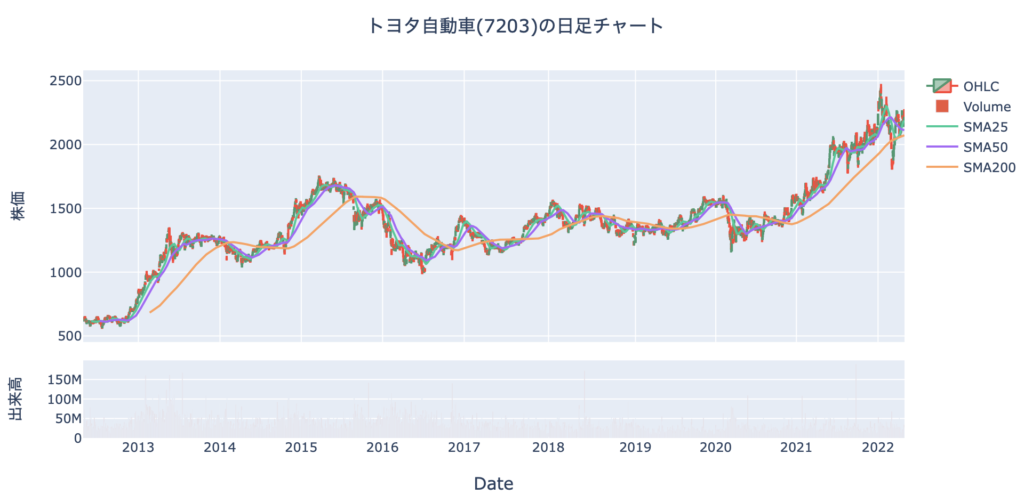
出来高も移動平均線もいい感じに表示できていますね。

期間が長すぎるせいで、出来高はかなり細くて見えにくいですがきちんと表示できています。

 

移動平均線乖離率を計算する

データの準備が整ったところで、本記事の本題である移動平均線乖離率を計算していきます。

 

終値と移動平均線から乖離率を計算

移動平均線乖離率を計算するには、株価終値と移動平均線を使います。

これらの乖離を求めればいいので、計算方法は次の通りです。

 

 

どちらで計算しても同じです。

これをPythonで実装すればOKです。

1行で簡単に計算できます。

 

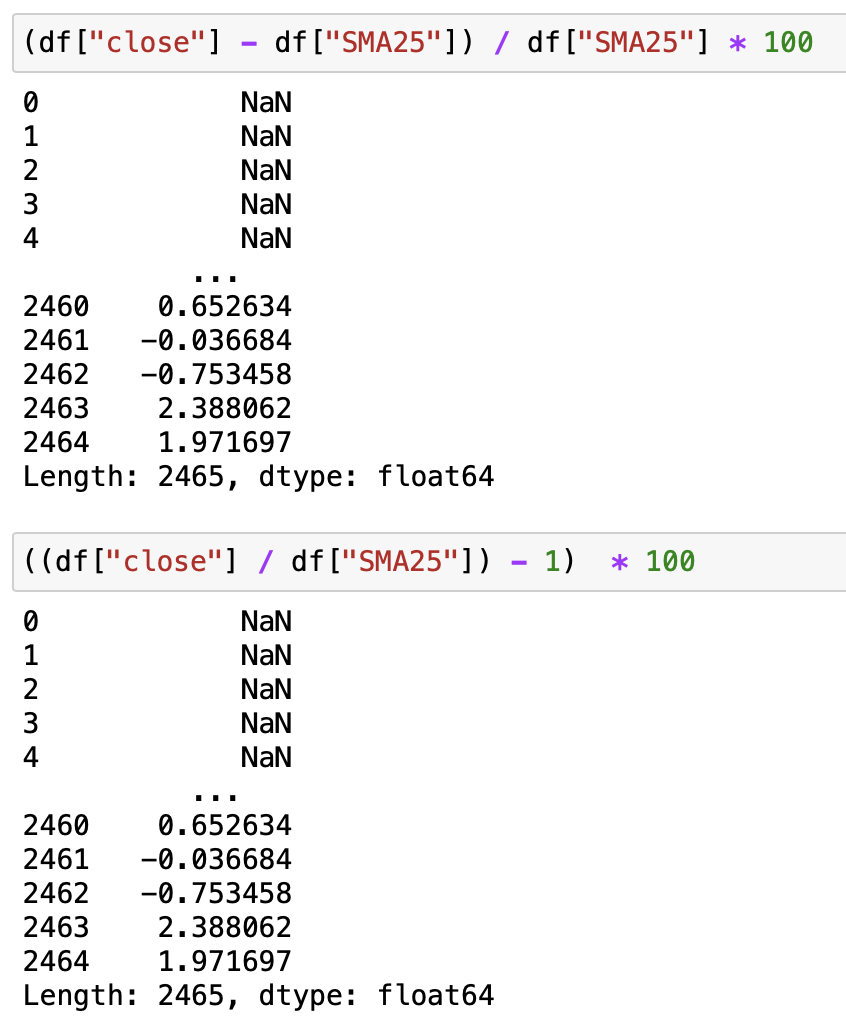
どちらを使ってもいいですが、ここでは1つ目のやり方を使います。

それぞれの移動平均線で計算すればOKです。

 

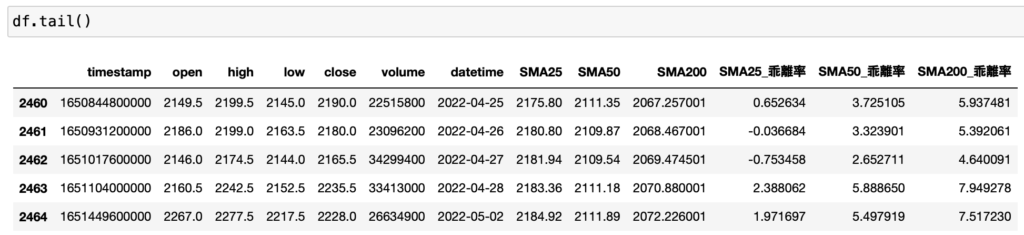
# 移動平均線乖離率
df["SMA25_乖離率"] = (df["close"] - df["SMA25"]) / df["SMA25"] * 100
df["SMA50_乖離率"] = (df["close"] - df["SMA50"]) / df["SMA50"] * 100
df["SMA200_乖離率"] = (df["close"] - df["SMA200"]) / df["SMA200"] * 100

 

きちんと計算できていることが確認できます。

 

移動平均線乖離率の特徴を見る

移動平均線乖離率の計算が完了したところで、この特徴についてみていきます。

まずはdescribe関数で基本的な統計データを見てみます。

 

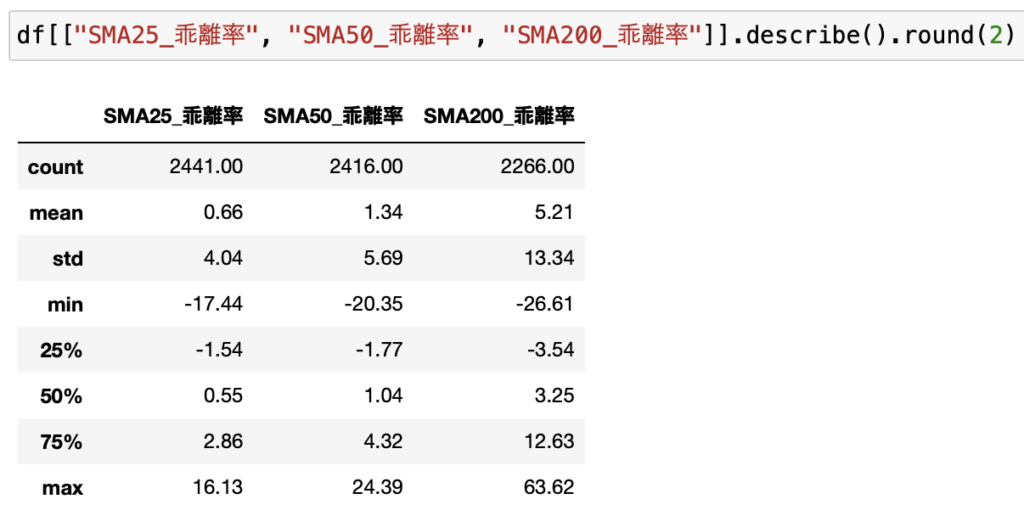
移動平均線は期間を延ばすほど滑らかになります。

そして期間が長くなるほど、株価との乖離が大きくなりがちです。

この特徴がデータとして確認できます。

平均値で見ても、標準偏差で見ても、中央値で見ても、期間が長くなるほどこれらの数値は大きくなっていきます。

 

次に移動平均線乖離率をヒストグラムで見てみます。

import seaborn as sns
import matplotlib.pyplot as plt
import japanize_matplotlib
%matplotlib inline

fig, ax = plt.subplots(1, 3, figsize=(15, 5))

sns.distplot(df["SMA25_乖離率"], ax=ax[0])
sns.distplot(df["SMA50_乖離率"], ax=ax[1])
sns.distplot(df["SMA200_乖離率"], ax=ax[2])

 

 

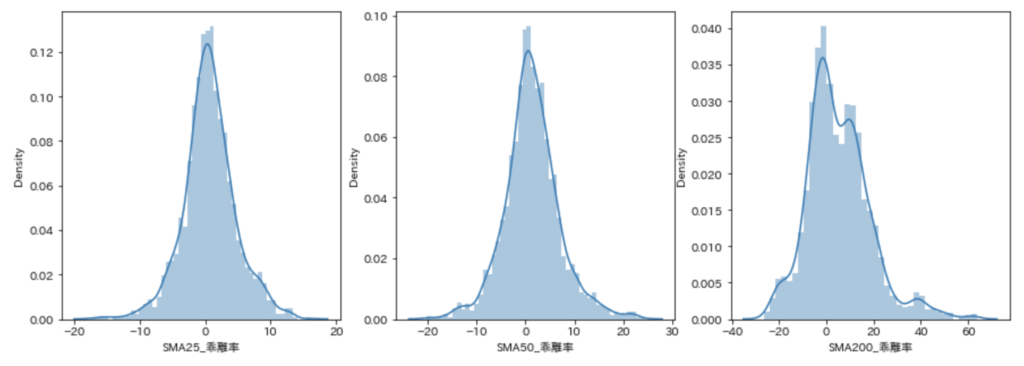
特に25日・50日移動平均線乖離率はきれいな正規分布になっていることがわかります。

200日移動平均線は少し歪な形です。

 

基本的に、移動平均線乖離率は0付近を中心とした正規分布になります

データが多ければ多いほど正規分布に近づきます。

200日移動平均線乖離率も、データを増やせば正規分布に近づくはずです。

 

買われすぎ・売られすぎの基準を決める

移動平均線乖離率は0付近を中心とする正規分布を形成します。

ここから言えるのは、乖離率が大きくなったら移動平均線に戻ってくるということです。

この特性を利用すれば、ある程度の乖離率に達したら、反転の兆しあるいは買われすぎ・売られすぎのサインであると判断することができます。

 

それではこのある程度の乖離率はどのように定義すればいいでしょうか。

これには色々な方法が考えられますが、ここでは正規分布の特徴を利用します。

正規分布を使えば、平均値と標準偏差から、全体のデータの割合を算出することができます。

 

平均値をm、標準偏差をσとすれば、正規分布のデータの割合は次のようになります。

 

これは、m±1σの範囲に収まる確率は約68％で、全体の68％のデータがm±1σに収まるという意味になります。

m±2σなら全体のおよそ95％を占め、これより外側にいるデータは全体の約5％しかありません。

この特徴を利用すれば、どの範囲を超えたら買われすぎ・売られすぎを判断することができます。

 

先ほどの統計データを使えば、これらを計算することができます。

 

このデータのmeanが平均値で、stdが標準偏差です。

例えば、25日移動平均線乖離率のm±2σを求めるなら、

0.66 ± (2 * 4.04) = -7.42 ~ 8.74になります。

この範囲内に全体の約95％が収まり、残り5％はこの範囲外にいることになります。

さらに正規分布は左右対称になるので、-7.42より左側には全体の約2.5%しかいません。

8.74より大きいものは全体の約2.5％です。

 

これを基準にすれば買われすぎ・売られすぎを判断することができます。

より厳しい条件で判断したいならをm±3σを使えばOKです。

 

試しに25日移動平均線でm±2σより外側にいるデータを抽出してみます。

 

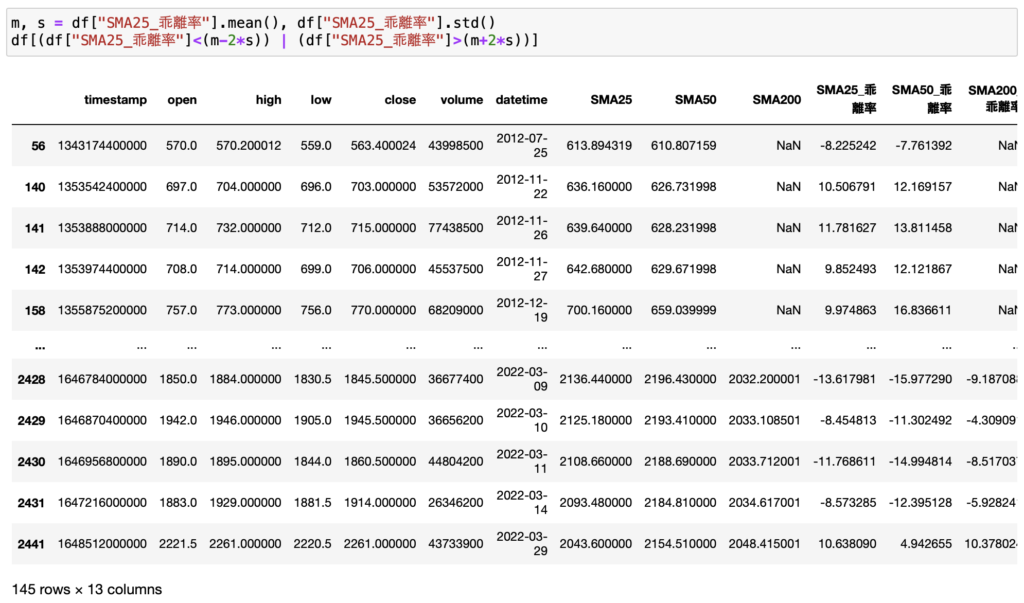
該当データが145個あることが確認できます。

全体のデータの割合を計算するとおよそ5.94％です。

少し差はありますが、おおむね理論通りになっています。

 

移動平均線乖離率をチャートに表示する

最後に、移動平均線乖離率をチャートに表示してみます。

さらに買われすぎ・売られすぎのシグナルも可視化してみます。

 

まずは普通に表示してみる

まずは普通に表示してみます。

移動平均線乖離率を表示するためにチャートを1つ加えます。

 

import pandas as pd
import plotly.graph_objects as go
from plotly.subplots import make_subplots
 
# 非表示にする日付をリストアップ
d_all = pd.date_range(start=df['datetime'].iloc[0],end=df['datetime'].iloc[-1])
d_obs = [d.strftime("%Y-%m-%d") for d in df['datetime']]
d_breaks = [d for d in d_all.strftime("%Y-%m-%d").tolist() if not d in d_obs]
 
# figを定義
fig = make_subplots(rows=3, cols=1, shared_xaxes=True, vertical_spacing=0.05, row_width=[0.2, 0.2, 0.7], x_title="Date")
 
# Candlestick 
fig.add_trace(
    go.Candlestick(x=df["datetime"], open=df["open"], high=df["high"], low=df["low"], close=df["close"], name="OHLC"),
    row=1, col=1
)
 
# Volume
fig.add_trace(
    go.Bar(x=df["datetime"], y=df["volume"], name="Volume"),
    row=2, col=1
)

# 乖離率
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["SMA25_乖離率"], name="SMA25_乖離率"),
    row=3, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["SMA50_乖離率"], name="SMA50_乖離率"),
    row=3, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["SMA200_乖離率"], name="SMA200_乖離率"),
    row=3, col=1
)

# SMA
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA25"], name="SMA25", mode="lines"), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA50"], name="SMA50", mode="lines"), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA200"], name="SMA200", mode="lines"), row=1, col=1)


 
# Layout
fig.update_layout(
    title={
        "text": "トヨタ自動車(7203)の日足チャート",
        "y":0.9,
        "x":0.5,
    }
)
 
# y軸名を定義
fig.update_yaxes(title_text="株価", row=1, col=1)
fig.update_yaxes(title_text="出来高", row=2, col=1)
fig.update_yaxes(title_text="乖離率", row=3, col=1)

 
# 不要な日付を非表示にする
fig.update_xaxes(
    rangebreaks=[dict(values=d_breaks)]
)
 
fig.update(layout_xaxis_rangeslider_visible=False)
fig.show()

 

 

表示されるチャートがこちらです。

 

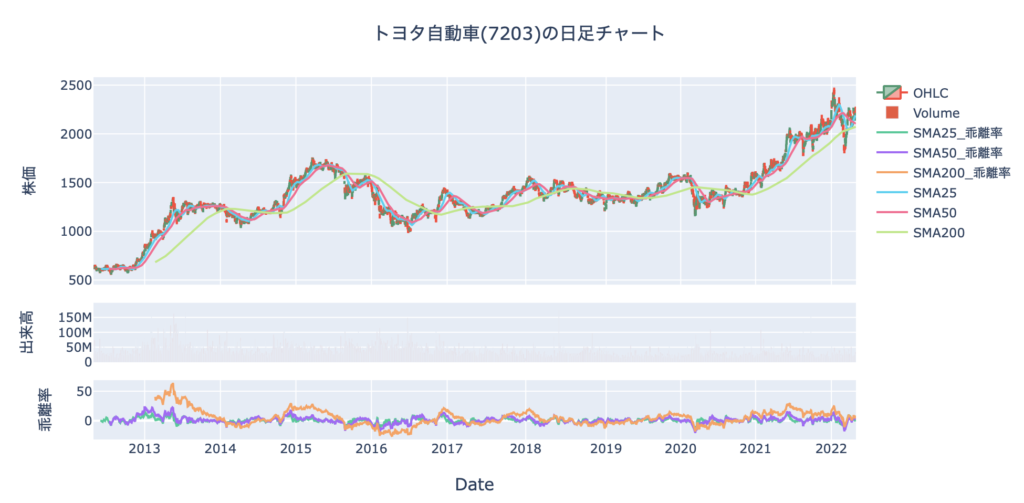
ここでは全ての移動平均線乖離率を表示していますが、見にくいので別々に表示するかあるいはどれか1つだけ表示すればいいかもですね。

とりあえずこれでチャートに表示ができました。

 

買われすぎ・売られすぎのサインを表示する

これが最後の仕上げです。

移動平均線乖離率から買われすぎ・売られすぎのサインを判定してチャートに表示してみます。

 

例として、先ほどご紹介した25日移動平均線乖離率のm±2σを使います。

これを求めると、0.66 ± (2 * 4.04) = -7.42 ~ 8.74でした。

つまり、使うサインは次の通りです。

 

 

これを使って買われすぎ・売られすぎのサインを判定し、チャートに加えていきます。

買われすぎは▼、売られすぎは▲で示します。

 

import pandas as pd
import plotly.graph_objects as go
from plotly.subplots import make_subplots

m, s = df["SMA25_乖離率"].mean(), df["SMA25_乖離率"].std()

# 非表示にする日付をリストアップ
d_all = pd.date_range(start=df['datetime'].iloc[0],end=df['datetime'].iloc[-1])
d_obs = [d.strftime("%Y-%m-%d") for d in df['datetime']]
d_breaks = [d for d in d_all.strftime("%Y-%m-%d").tolist() if not d in d_obs]
 
# figを定義
fig = make_subplots(rows=3, cols=1, shared_xaxes=True, vertical_spacing=0.05, row_width=[0.2, 0.2, 0.7], x_title="Date")
 
# Candlestick 
fig.add_trace(
    go.Candlestick(x=df["datetime"], open=df["open"], high=df["high"], low=df["low"], close=df["close"], name="OHLC"),
    row=1, col=1
)
 
# Volume
fig.add_trace(
    go.Bar(x=df["datetime"], y=df["volume"], name="Volume"),
    row=2, col=1
)

# 乖離率
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["SMA25_乖離率"], name="SMA25_乖離率"),
    row=3, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["SMA50_乖離率"], name="SMA50_乖離率"),
    row=3, col=1
)
fig.add_trace(
    go.Scatter(x=df["datetime"], y=df["SMA200_乖離率"], name="SMA200_乖離率"),
    row=3, col=1
)

# 買われすぎ
fig.add_trace(go.Scatter(x=df[df["SMA25_乖離率"]>(m+(2*s))]["datetime"], y=df[df["SMA25_乖離率"]>(m+(2*s))]["close"]*1.02, name="買われすぎ", mode="markers", marker_symbol="triangle-down", marker_size=5, marker_color="black"), row=1, col=1)
 
# 売られすぎ
fig.add_trace(go.Scatter(x=df[df["SMA25_乖離率"]<(m-(2*s))]["datetime"], y=df[df["SMA25_乖離率"]<(m-(2*s))]["close"]*0.98, name="売られすぎ", mode="markers", marker_symbol="triangle-up", marker_size=5, marker_color="black"), row=1, col=1)


# SMA
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA25"], name="SMA25", mode="lines"), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA50"], name="SMA50", mode="lines"), row=1, col=1)
fig.add_trace(go.Scatter(x=df["datetime"], y=df["SMA200"], name="SMA200", mode="lines"), row=1, col=1)


 
# Layout
fig.update_layout(
    title={
        "text": "トヨタ自動車(7203)の日足チャート",
        "y":0.9,
        "x":0.5,
    }
)
 
# y軸名を定義
fig.update_yaxes(title_text="株価", row=1, col=1)
fig.update_yaxes(title_text="出来高", row=2, col=1)
fig.update_yaxes(title_text="乖離率", row=3, col=1)

 
# 不要な日付を非表示にする
fig.update_xaxes(
    rangebreaks=[dict(values=d_breaks)]
)
 
fig.update(layout_xaxis_rangeslider_visible=False)
fig.show()

きちんと表示されていることが確認できますね。

これをうまく活用することができれば、利益を出すことができるのではないでしょうか。

 

しかし、結果を見てると少し気になる部分が見えてきます。

それは、買われすぎ・売られすぎサインは連続して出てくることがあるということです。

強い上昇局面や下落局面では、これらのサインは連日出てきます。

 

よって、これに従って逆張りとかをしていたら大損失を被ることになります。

利確のタイミングで使うと少しの利益を取ることはできても、かなりの利益を逃すことになります。

この辺りは少し工夫が必要になりそうです。

 

ちなみに、m±3σにすると、サインはかなり減ります。

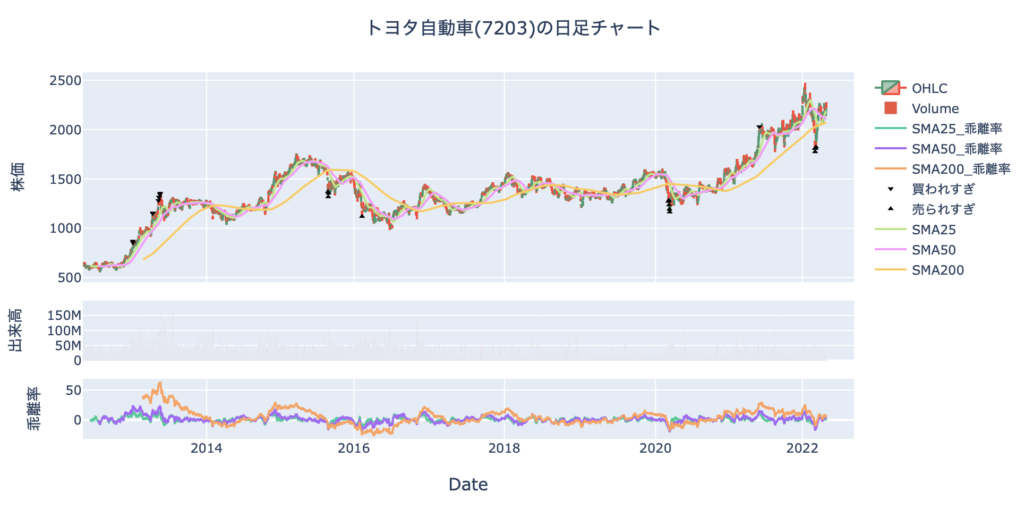
これならこのままでもある程度は活用できそうです。

しかし、頻度が激減してしまうので売買回数は大きく減ってしまいます。

もし使うなら投資対象銘柄を増やしていくとかしないといけないですね。

 

ゴールデンクロスや移動平均線の押し目や上放れなどでエントリーして、買われすぎのサインで利確するみたいなやり方もそれなりにうまくいくかもしれません。

使い方を見出すことができればがっぽり稼げるかもしれません。

また、銘柄によって値動きの特徴は異なるので、全てのやり方が全銘柄に適用できるとは思いません。

ここでは25日移動平均線で乖離率を算出しましたが、この期間を変更したり、基準値も調整が必要になってきます。

色々な検証が必要です。

 

いつかいろんな銘柄で売買シミュレーションしてみたいですね。

 

データの分析・可視化にはPythonが最適！

本記事で紹介したコードは、全てPythonを使って書いています。

 

Pythonはデータの分析や可視化を得意とするプログラミング言語で、さらにAI関連のライブラリーも豊富で昨今のAIブームで需要が急拡大しています。

→ 【いますぐ始められます】データ分析をするならPythonが最適です。

 

また、Pythonは比較的学びやすい言語でもあります。

実際、僕は社会人になってからPythonを独学で習得して転職にも成功し、Python独学をきっかけに人生が大きく変わりました。

→ 【実体験】ゼロからのPython独学を決意してから転職を掴み取るまでのお話。 

 

Pythonの学習方法についてはいろいろな方法があります。

僕はUdemyを選びましたが、書籍やプログラミングスクールも選択肢になります。

→ 【決定版】Python独学ロードマップ【完全初心者からでもOKです】

→ 【まとめ】Pythonが学べるおすすめプログラミングスクール

→ プログラミングの独学にUdemyをおすすめする理由！【僕はUdemyでPythonを独学しました！】

 

 

まとめ

いかがでしたでしょうか。

ここでは「【Pythonで株式投資】移動平均線乖離率を計算して「買われすぎ・売られ過ぎ」を判定する」というテーマでPythonで移動平均線乖離率を計算して、買われすぎ・売られすぎのサインを判定する方法について解説しました。

さらにチャートでこれらのサインを可視化する方法についても解説しました。

 

今後も「Python × 株式投資」に関する記事は増やしていこうと思います。

色々なテクニカル分析をPythonで実装したり、可視化したり、売買シミュレーションをしてみたり、僕がチコチコやった作業を紹介したり解説していこうと思います。

もしリクエストとかありましたらご連絡ください！

 

ここまで読んでくださり、ありがとうございました。