こんにちは。TATです。
今日のテーマは「【コード解説】Pythonで株価データから主要なテクニカル分析を計算して可視化する【移動平均線、MACD、RSI】」です。
株価データを使って各種テクニカル分析をPythonを用いて計算してみます。
もちろんコードもすべて公開していきます。
様々なテクニカル分析がありますが、本記事では僕が普段特に使っている移動平均線、MACD、RSIに絞りました。
また、ここで紹介しているコードはあくまで一例にすぎないので、ご自由にパクリつつ、適宜改善していっちゃってください！
そしてミス等ありましたら教えていただけると嬉しいです。
目次
【コード解説】Pythonで株価データから主要なテクニカル分析を計算して可視化する【移動平均線、MACD、RSI】
（おさらい）株価データを取得する
まずはおさらいとして、計算に必要な株価データを取得します。
ここは過去に記事でも解説しているので詳細は割愛します。
今回はpandas_datareaderを使ってトヨタ（7203）の株価データを取得します。
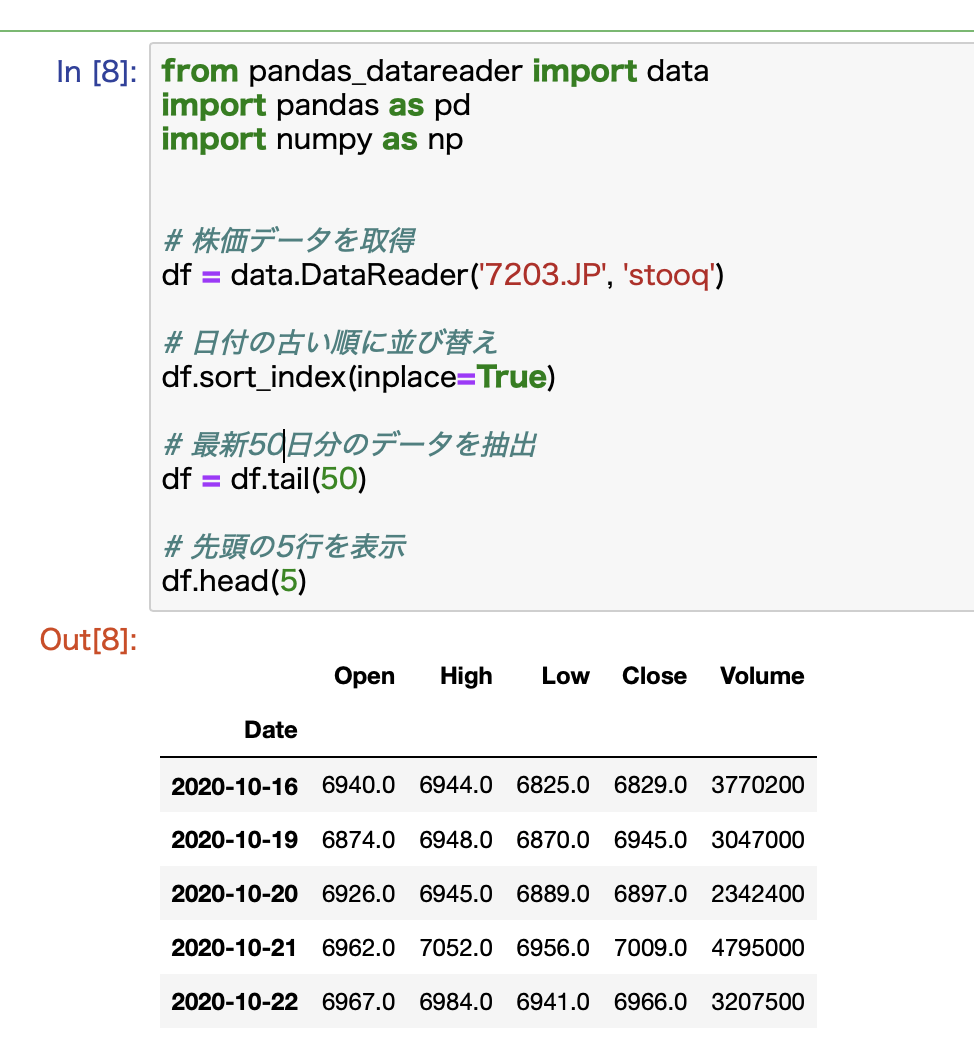
1 2 3 4 5 6 7 8 9 | from pandas_datareader import data import pandas as pd import numpy as np # 株価データを取得 df = data.DataReader('7203.JP', 'stooq') # 日付の古い順に並び替え df.sort_index(inplace=True) |
このコードで取得した株価データはこんな感じです。
このままだとデータ数が多いので、直近50日のデータに絞ります。
このデータを使っていくつかのテクニカル分析を計算していきます。
Pythonで株価データを取得する方法についてはこちらの記事で解説しているので参考にしてください。
-
【日本株対応】Pythonで株価のローソク足データを取得する方法まとめ【CSV、ライブラリ、スクレイピング】
-
【Pythonコード解説】yahoo_finance_api2で日本株の株価データを取得する
続きを見る
移動平均線
まずはテクニカル分析で最も基本となる移動平均線です。
移動平均線の使い方についてはこちらの記事で解説しているのでよろしければご覧ください。
-
【シンプルだけど奥深い！】「移動平均線」について 徹底解説します！
コードを公開
移動平均線は、pandasのrolling関数を使えば一瞬で計算できます。
コードもシンプルなので一目でわかるかと思います。
ここでは5日移動平均線・25日移動平均線を計算しています。
1 2 | df["SMA5"] = df["Close"].rolling(window=5).mean() df["SMA25"] = df["Close"].rolling(window=25).mean() |
ご覧の通りです。
終値で計算するので、Close列を指定してrolling関数を適用します。
そして引数のwindowで期間を指定します。
最後に平均値を指定するmean()をつければおしまいです。
ここをmax()とかmin()にすると、その期間のおける最高値あるいは最安値を計算することもできます。
計算結果を確認
計算結果はこんな感じです。
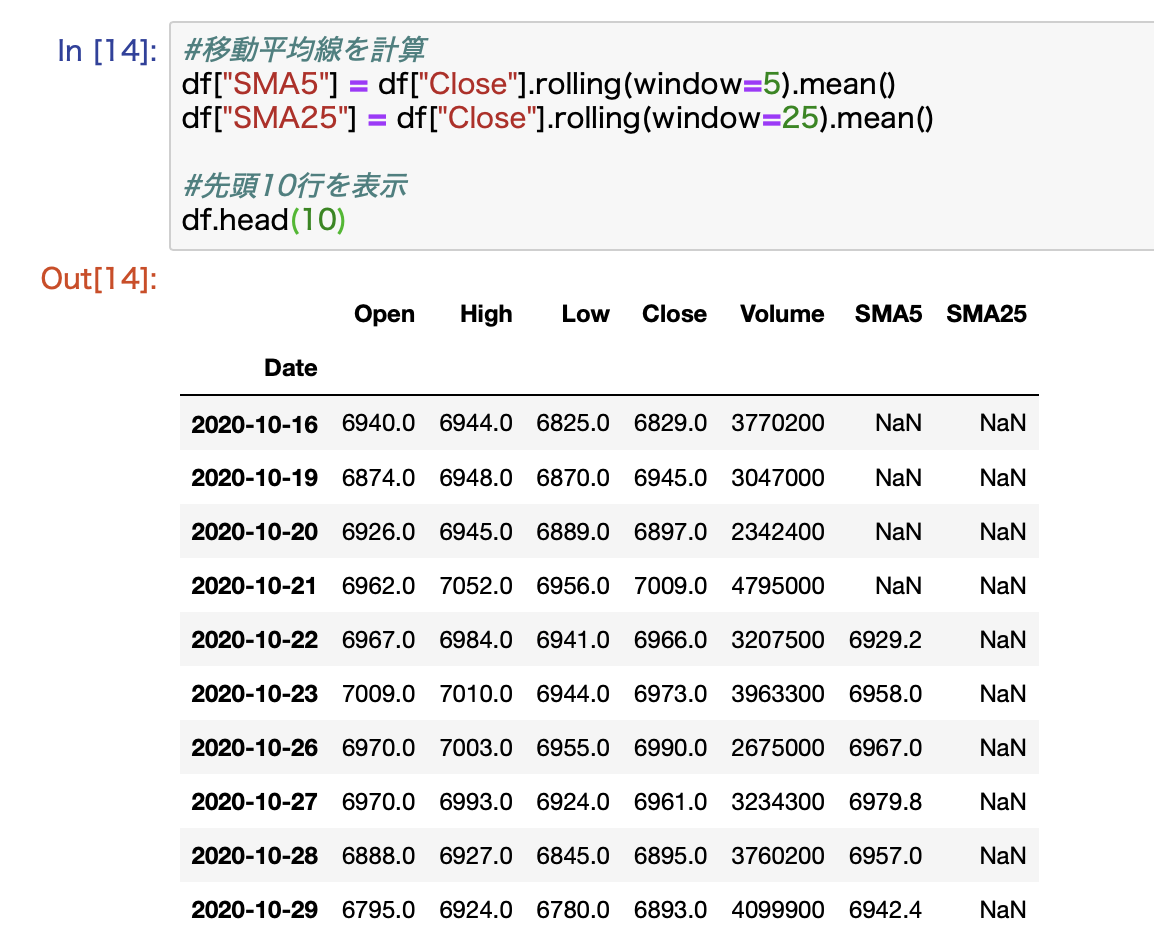
きちんと計算されていることがわかりますね。
期間が不十分の場合はNaNとなっています。
この辺のいい感じに計算してくれちゃうのがPythonの素晴らしいところです。
グラフに描く
算出した移動平均線をグラフ化するときちんと計算できていることが確認できます。
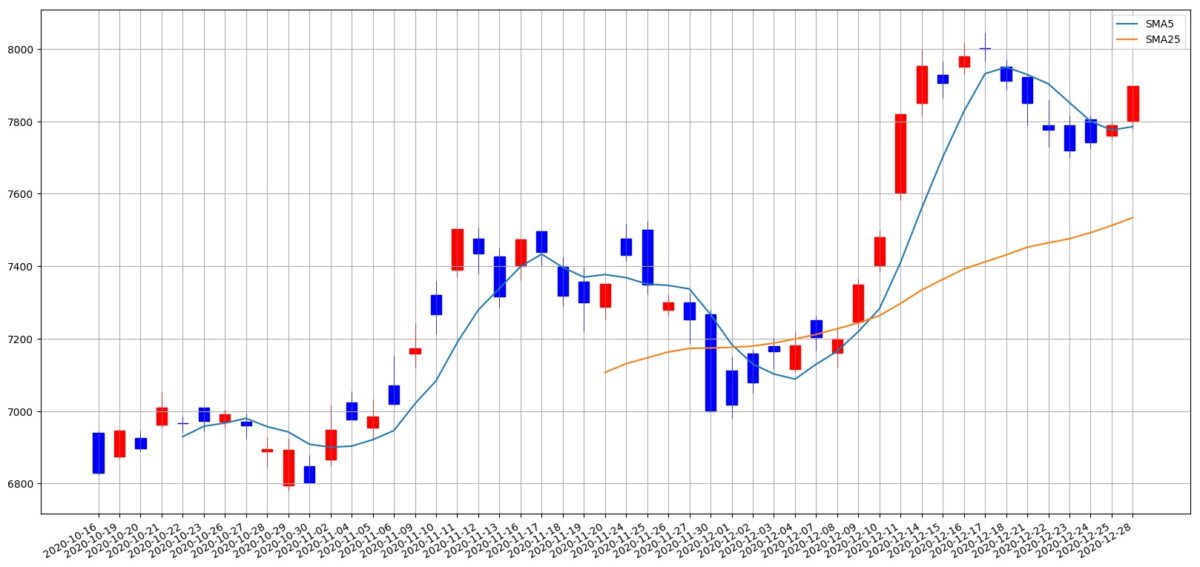
ちなみにこちらのグラフを描いたコードはこちらです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | import mpl_finance import matplotlib.pyplot as plt %matplotlib inline # チャート定義 fig, ax = plt.subplots(figsize=(20, 10)) # ローソク足チャートをプロット mpl_finance.candlestick_ohlc(ax, df.values, width=0.5, colorup='r', colordown='b') # 移動平均線をプロット ax.plot(df["index"], df["SMA5"], label="SMA5") ax.plot(df["index"], df["SMA25"], label="SMA25") # X軸を調整 plt.xticks([x for x in range(len(df))], [x.strftime('%Y-%m-%d') for x in df.index]) fig.autofmt_xdate() # 凡例表示 plt.legend() # グリッド表示 plt.grid() # グラフを表示 plt.show() |
このチャートを書くためにindexというコラムを追加しています。
これは単純に1行目から0から順にカウントしているだけで、一列目に追加しています。
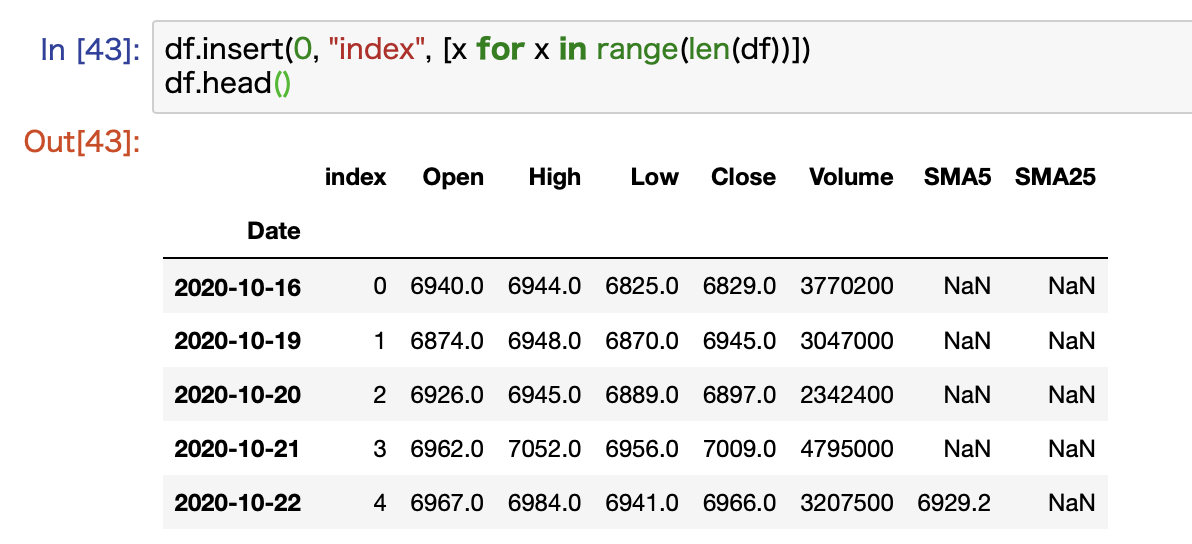
グラフの書き方についてはこちらの記事で詳しく解説しています。
-
Pythonのmpl_financeで株価のローソク足チャートを描く方法【コード解説】
MACD
次にMACDをご紹介します。
MACDは2種類の指数平滑移動平均（通常は12と26）の差分を計算して、さらにその差分の移動平均（通常は9）を求めることで算出できます。
MACDはトレンド系とオシレーター系の両方の特徴を併せ持つ人気のテクニカル分析手法です。
過去記事でも紹介しており、僕も愛用しています。
-
【最も人気なツールの1つ】 「MACD」について徹底解説！
コードを公開
それではコードをどうぞ。今回はMACDを計算する関数を作ってみました。
1 2 3 4 5 6 7 8 9 10 | def macd(df): FastEMA_period = 12 # 短期EMAの期間 SlowEMA_period = 26 # 長期EMAの期間 SignalSMA_period = 9 # SMAを取る期間 df["MACD"] = df["Close"].ewm(span=FastEMA_period).mean() - df["Close"].ewm(span=SlowEMA_period).mean() df["Signal"] = df["MACD"].rolling(SignalSMA_period).mean() return df # MACDを計算する df = macd(df) |
関数内でMACDに使う変数を自由に設定できるようにしました。
期間を変えたい場合はこれらの変数を弄ればOKです。
ewa関数を使うと指数平滑移動平均を一瞬で計算できるので便利です。
計算結果を確認
計算結果を確認します。
こんな感じできちんと計算できています。
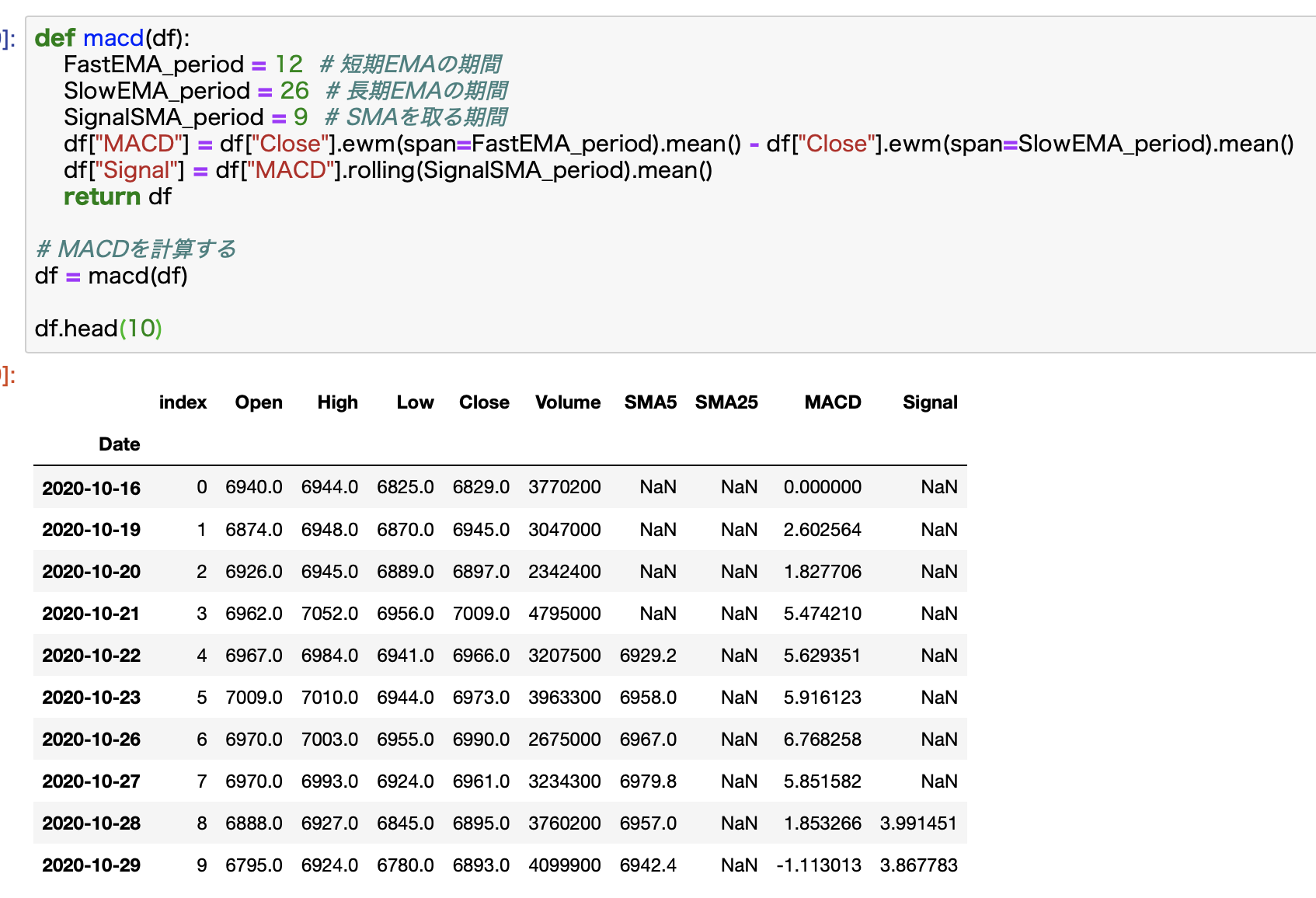
グラフに描く
計算したMACDをグラフで確認します。
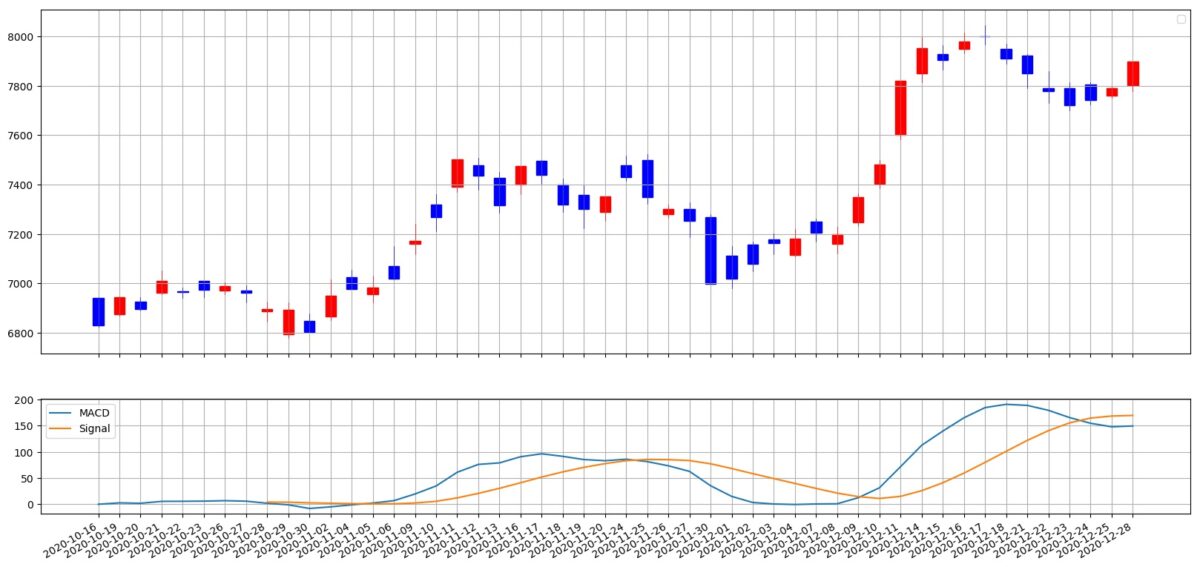
こちらのグラフのソースコードがこちらです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | import mpl_finance import matplotlib.pyplot as plt %matplotlib inline # チャート定義 fig, ax = plt.subplots(2, figsize=(20, 10), sharex=True, gridspec_kw={'height_ratios': [3, 1]}) # ローソク足チャートをプロット mpl_finance.candlestick_ohlc(ax[0], df.values, width=0.5, colorup='r', colordown='b') # MACDをプロット ax[1].plot(df["index"], df["MACD"], label="MACD") ax[1].plot(df["index"], df["Signal"], label="Signal") # X軸を調整 plt.xticks([x for x in range(len(df))], [x.strftime('%Y-%m-%d') for x in df.index]) fig.autofmt_xdate() # 凡例表示, グリッド表示 for a in ax: a.legend() a.grid() # グラフを表示 plt.show() |
subplots関数を使うとグラフを分割して複数の種類のグラフをまとめて表示することが可能になります。
-
Pythonのmpl_financeで株価のローソク足チャートを描く方法【コード解説】
RSI
最後にRSIを見ていきます。
RSIはオシレーター系の代表的なテクニカル分析手法で、株価の上がりすぎや下がりすぎを判断するために使われます。
一般的に期間は14が用いられ、この期間で平均上がり幅と平均値下がり幅の比で算出されます。
0〜100の数値で示され、50を超えると上昇平均の方が大きいことを意味します。
一般的に70で買われすぎ、30で売られすぎと判断され、逆張りに利用されることが多いです。
過去の記事では僕独自の使い方もすべて公開しているので是非ともご覧いただけると嬉しいです。
-
【オシレーター系の定番！】RSIについて徹底解説！【僕の独自活用法も公開】
コードを公開
それではRSIを計算するPythonコードをどうぞ。
ちょっと長いです。
もっとコンパクトに書ける方法があれば教えていただけると嬉しいです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | def rsi(df): # 前日との差分を計算 df_diff = df["Close"].diff(1) # 計算用のDataFrameを定義 df_up, df_down = df_diff.copy(), df_diff.copy() # df_upはマイナス値を0に変換 # df_downはプラス値を0に変換して正負反転 df_up[df_up < 0] = 0 df_down[df_down > 0] = 0 df_down = df_down * -1 # 期間14でそれぞれの平均を算出 df_up_sma14 = df_up.rolling(window=14, center=False).mean() df_down_sma14 = df_down.rolling(window=14, center=False).mean() # RSIを算出 df["RSI"] = 100.0 * (df_up_sma14 / (df_up_sma14 + df_down_sma14)) return df # RSIを算出 df = rsi(df) |
ちょっとややこしいので解説しておくと、まずは前日との差分を計算してdf_diffに格納します。
これをcopyしてdf_upとdf_downを定義します。
それぞれ、値上がりと値下がりの平均を計算するために使います。
df_upはマイナス値を0に変換、df_downはプラス値を0に変換します。
さらにその後はdf_downの数値の正負を反転するために-1をかけます。
あとは平均値を計算して比を算出すれば完成です。
計算結果を確認
計算結果を確認します。
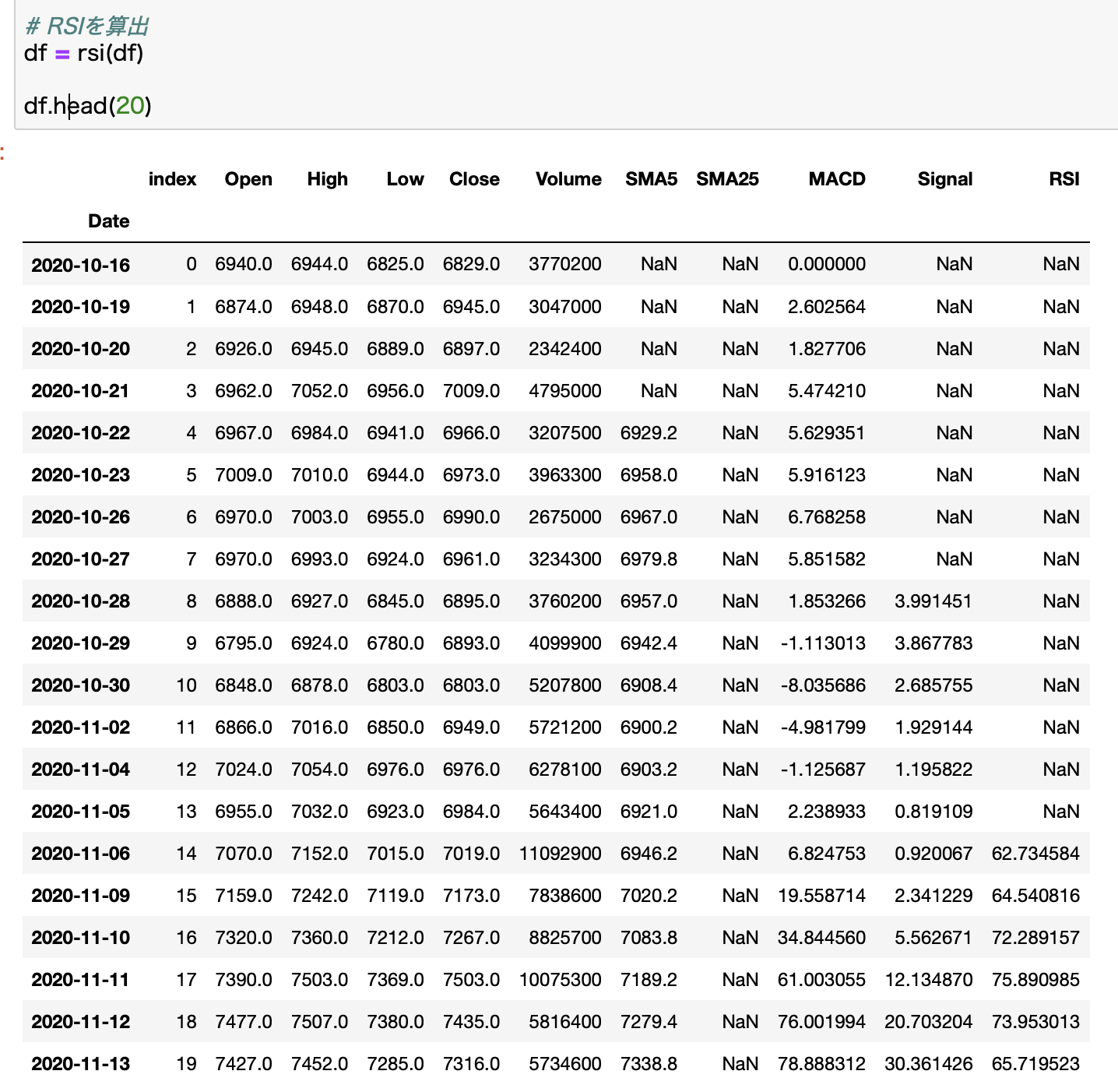
RSIの使い方についてはこちらの記事をどうぞ。僕独自の活用法も公開しています。
-
【オシレーター系の定番！】RSIについて徹底解説！【僕の独自活用法も公開】
グラフに描く
最後に算出したRSIをグラフで確認します。
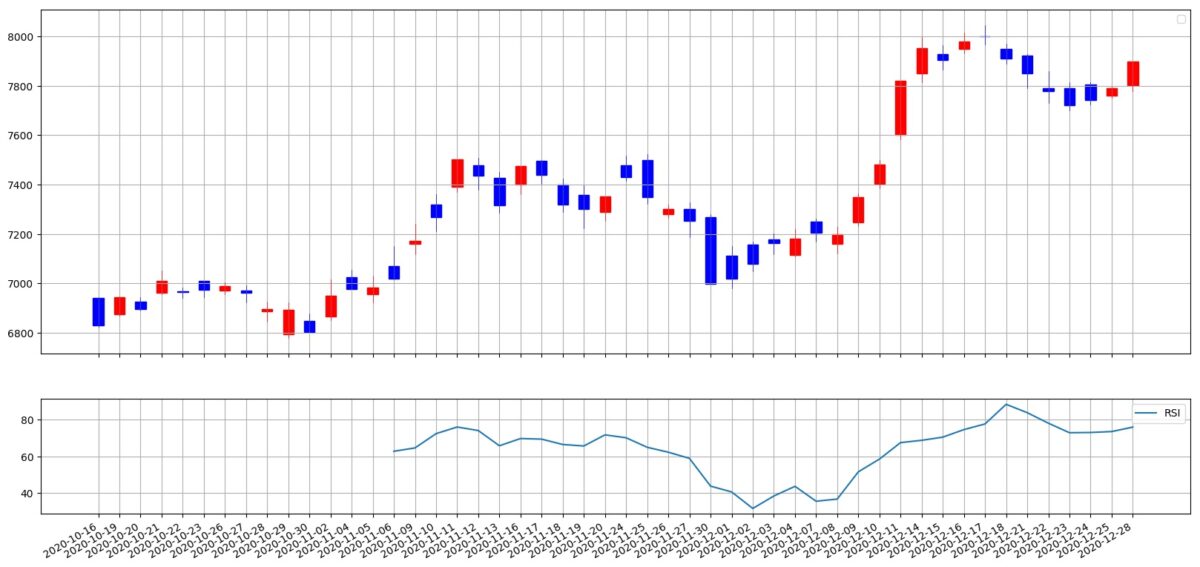
このチャートを描くためのソースコードがこちらです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | import mpl_finance import matplotlib.pyplot as plt %matplotlib inline # チャート定義 fig, ax = plt.subplots(2, figsize=(20, 10), sharex=True, gridspec_kw={'height_ratios': [3, 1]}) # ローソク足チャートをプロット mpl_finance.candlestick_ohlc(ax[0], df.values, width=0.5, colorup='r', colordown='b') # RSIをプロット ax[1].plot(df["index"], df["RSI"], label="RSI") # X軸を調整 plt.xticks([x for x in range(len(df))], [x.strftime('%Y-%m-%d') for x in df.index]) fig.autofmt_xdate() # 凡例表示, グリッド表示 for a in ax: a.legend() a.grid() # グラフを表示 plt.show() |
こちらもMACDの時の同様にグラフを分割してRSIを表示しています。
このあたりのカスタマイズはmatplotlibを使うと柔軟にできるので、使いこなせるととても便利です。
-
Pythonのmpl_financeで株価のローソク足チャートを描く方法【コード解説】
データの分析・可視化にはPythonが最適！
本記事で紹介したコードは、全てPythonを使って書いています。
Pythonはデータの分析や可視化を得意とするプログラミング言語で、さらにAI関連のライブラリーも豊富で昨今のAIブームで需要が急拡大しています。
→ 【いますぐ始められます】データ分析をするならPythonが最適です。
また、Pythonは比較的学びやすい言語でもあります。
実際、僕は社会人になってからPythonを独学で習得して転職にも成功し、Python独学をきっかけに人生が大きく変わりました。
→ 【実体験】ゼロからのPython独学を決意してから転職を掴み取るまでのお話。
Pythonの学習方法についてはいろいろな方法があります。
僕はUdemyを選びましたが、書籍やプログラミングスクールも選択肢になります。
→ 【決定版】Python独学ロードマップ【完全初心者からでもOKです】
→ 【まとめ】Pythonが学べるおすすめプログラミングスクール
→ プログラミングの独学にUdemyをおすすめする理由！【僕はUdemyでPythonを独学しました！】
まとめ
いかがでしたでしょうか。
今回は「【コード解説】Pythonで株価データから主要なテクニカル分析を計算して可視化する【移動平均線、MACD、RSI】」というテーマで、移動平均線・MACD・RSIの計算方法について紹介しました。
これらは僕が普段の株式投資でよく利用しているものです。
Pythonはデータ分析に最適な言語で、株価データの分析も容易に実装できます。
本記事でご紹介したコードを活用して、株式投資に役立てていただけたら嬉しいです。
ここまで読んでくださってありがとうございました。
